- ...
方程式を解く方法について学びます1
- 方程式を難しくする「原因」として、
非線型性と無限次元性がある。ここでは非線型性を取り上げる。
なお、有限次元の線型方程式 (いわゆる未知数有限個の連立1次方程式)
が簡単と言っているわけではない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
線形方程式以外は例外的な状況をのぞいて解けない2
- 「例外的な状況」は重要でないと勘違いしないように。
解けるような例外的な問題には重要なものも多い。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... にあることが分かります3
- まず
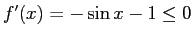 (
(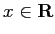 ) で、特に
) で、特に
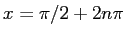 (
(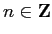 ) 以外のところでは
) 以外のところでは 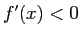 であるから、
であるから、
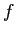 は狭義の単調減少関数である。
そして
は狭義の単調減少関数である。
そして 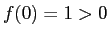 ,
,
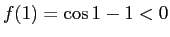 ゆえ、
中間値の定理によって、
方程式
ゆえ、
中間値の定理によって、
方程式 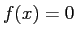 は区間
は区間 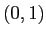 内に少なくとも1つの解を持つが、
内に少なくとも1つの解を持つが、
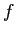 の単調性からそれは
の単調性からそれは 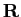 全体でただ1つの解であることが分かる。
全体でただ1つの解であることが分かる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (原子炉圧力容器の構造計算とか4
- 本来は、
偏微分方程式で、未知数の個数は無限というべき問題だが、適当な離散化により、
有限次元の問題になる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... とほとんど差がない5
- 実際、
連立1次方程式の解を求めるために、
Gauss の消去法などの exact な計算法が知られているが、
CG 法 (共役勾配法) などの反復法が採用されることも多い。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 6
6
- ここで引き合いに出すのは、
少々こじつけかもしれないが、
アルキメデス (BC 287-212, シラクサに生まれ、
シラクサに没する) の『方法』に書いてあるという言葉
「ある種の問題は、まず工学的な方法で答が明らかになってしまう。
もちろん後で幾何学的に証明を付けなくてはいけないのだけれども、
それでも最初から答がわかっているのと、一から考えなくては
ならないのとでは雲泥の差がある」-- 木村俊一, 『天才数学者はこう解いた、
こう生きた』、講談社から引用。つまり 2000 年の歴史のある言い訳。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 7
7
- 杉原正顯、
室田一雄、『数値計算法の数理』、岩波書店などを見よ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...論よりrunで行ってみましょう8
- BASIC では、
プログラムを動かすことを「run させる (走らせる)」と言うことがあります。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... を定めると、適当な条件9
- Newton 法が収束するための十分条件は色々知られているが、
ここでは説明しません。
簡単なものは微分積分学のテキストに載っていることもありますが、
山本哲朗『数値解析入門』サイエンス社 (2003) がお勧め。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.