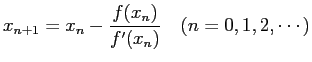

Next: 3.8 二分法 vs. Newton
Up: 3 方程式の数値解法
Previous: 3.6 Newton 法
(情報処理教室で実習中にここを読む時間はほとんどないでしょうから、
余裕のあるときに読んで下さい。)
Newton 法は非線形方程式を解くための代表的な方法です。
これは 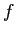 が微分可能な関数で、
方程式
が微分可能な関数で、
方程式 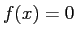 の近似解
の近似解 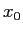 が得られているとき、線形化写像
が得られているとき、線形化写像
の零点
![$ x=x_0-\left[f'(x_0)\right]^{-1}f(x_0)$](img78.png) は、
は、
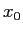 よりも良い近似解になっているだろう
(実際に適当な条件下でこれは正当化できます)、
という考えから導かれるものです。
よりも良い近似解になっているだろう
(実際に適当な条件下でこれは正当化できます)、
という考えから導かれるものです。
すなわち、漸化式
で数列
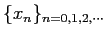 を定めると、適当な条件
9の下で
を定めると、適当な条件
9の下で
と収束し、極限 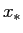 は方程式の解になっている:
は方程式の解になっている:
ということを利用したもので、実際のアルゴリズムは次のようになります。
| Newton法のアルゴリズム |
- (1)
- 適当な初期値
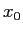 を選ぶ。
を選ぶ。
- (2)
-
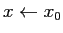
- (3)
-
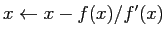 とする。
とする。
- (4)
- まだ近似の程度が十分でないと判断されたら (3) に戻る。
そうでなければ
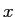 を解として出力する。
を解として出力する。
|


Next: 3.8 二分法 vs. Newton
Up: 3 方程式の数値解法
Previous: 3.6 Newton 法
桂田 祐史
2012-05-16
![]() が微分可能な関数で、
方程式
が微分可能な関数で、
方程式 ![]() の近似解
の近似解 ![]() が得られているとき、線形化写像
が得られているとき、線形化写像