(сЂЊсЂ«у»ђсЂ«тєЁт«╣сЂ»сЂЙсЂауи┤сѓЅсѓїсЂдсЂёсЂфсЂёсђѓ)
- (1)
-
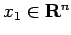 ,
,
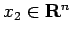
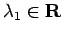 ,
,
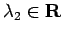 сЂе
сЂЎсѓІсђѓ
сЂе
сЂЎсѓІсђѓ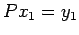 ,
, 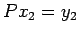 сЂеуй«сЂЊсЂєсђѓС╗«т«џсЂІсѓЅ
сЂеуй«сЂЊсЂєсђѓС╗«т«џсЂІсѓЅ
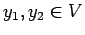 сЂІсЂц
сЂІсЂц
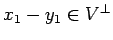 ,
,
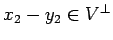 . сЂЊсЂ«сЂесЂЇсђЂ
. сЂЊсЂ«сЂесЂЇсђЂ
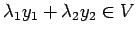 сЂІсЂц
сЂІсЂц
сѓєсЂѕсЂФ
- (2)
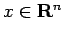 сЂесЂЎсѓІсЂесЂЇсђЂ
сЂесЂЎсѓІсЂесЂЇсђЂ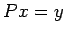 сЂеуй«сЂЊсЂєсђѓ
сЂеуй«сЂЊсЂєсђѓ ,
,
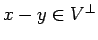 сЂД
сЂѓсѓІсђѓТўјсѓЅсЂІсЂФ
сЂД
сЂѓсѓІсђѓТўјсѓЅсЂІсЂФ  ,
,
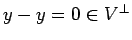 сЂДсЂѓсѓІсЂІсѓЅсђЂ
сЂДсЂѓсѓІсЂІсѓЅсђЂ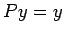 . сЂЎсЂфсѓЈ
сЂА
. сЂЎсЂфсѓЈ
сЂА 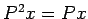 . сѓєсЂѕсЂФ
. сѓєсЂѕсЂФ 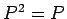 .
.
- (3)
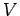 сЂ«ТГБУдЈуЏ┤С║цтЪ║т║Ћ
сЂ«ТГБУдЈуЏ┤С║цтЪ║т║Ћ 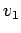 ,
,  ,
, 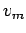 сѓњтЈќсѓІсЂе
сѓњтЈќсѓІсЂе
сѓєсЂѕсЂФ
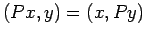 . сЂЊсѓїсЂ»
. сЂЊсѓїсЂ» 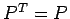 сѓњТёЈтЉ│сЂЎсѓІсђѓ
сѓњТёЈтЉ│сЂЎсѓІсђѓ 
т«ЪсЂ» 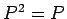 ,
, 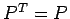 сЂесЂёсЂєТЮАС╗ХсѓњТ║ђсЂЪсЂЎ
сЂесЂёсЂєТЮАС╗ХсѓњТ║ђсЂЪсЂЎ 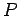 сЂ»жЂЕтйЊсЂфуиџтъІжЃетѕєуЕ║жќЊ
сЂ»жЂЕтйЊсЂфуиџтъІжЃетѕєуЕ║жќЊ 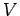 сЂИсЂ«уЏ┤С║цт░ётй▒Сйюућеу┤асЂФсЂфсѓІсђѓ
сЂИсЂ«уЏ┤С║цт░ётй▒Сйюућеу┤асЂФсЂфсѓІсђѓ
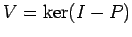 сЂ»ТўјсѓЅсЂІсЂФ
сЂ»ТўјсѓЅсЂІсЂФ 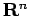 сЂ«уиџтъІжЃетѕєуЕ║жќЊсЂДсЂѓсѓІсђѓ
сЂ«уиџтъІжЃетѕєуЕ║жќЊсЂДсЂѓсѓІсђѓ
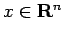 сЂФт»ЙсЂЌсЂд
сЂФт»ЙсЂЌсЂд 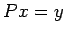 сЂесЂісЂЈсђѓ
С╗«т«џ
сЂесЂісЂЈсђѓ
С╗«т«џ 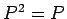 сѓѕсѓісђЂ
сѓѕсѓісђЂ
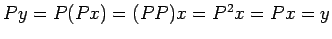 сЂДсЂѓсѓІсЂІсѓЅсђЂ
сЂДсЂѓсѓІсЂІсѓЅсђЂ сЂ«т«џуЙЕсЂФсѓѕсЂБсЂд
сЂ«т«џуЙЕсЂФсѓѕсЂБсЂд  .
сЂЙсЂЪ
.
сЂЙсЂЪ
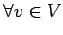 сЂФт»ЙсЂЌсЂд
сЂФт»ЙсЂЌсЂд  сЂФТ│еТёЈсЂЎсѓІсЂе
сЂФТ│еТёЈсЂЎсѓІсЂе
сЂЎсЂфсѓЈсЂА
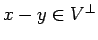 . сѓєсЂѕсЂФ
. сѓєсЂѕсЂФ 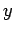 сЂ»
сЂ» 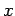 сЂ«
сЂ« 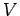 сЂИсЂ«уЏ┤С║цт░ётй▒сЂДсЂѓсѓІсђѓ
сЂИсЂ«уЏ┤С║цт░ётй▒сЂДсЂѓсѓІсђѓ

сЂЊсѓїсЂІсѓЅтЇўсЂФ 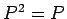 ,
, 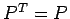 сѓњТ║ђсЂЪсЂЎ
сѓњТ║ђсЂЪсЂЎ
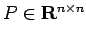 сЂ«сЂЊсЂесѓњ
уЏ┤С║цт░ётй▒Сйюућеу┤асЂеУеђсЂБсЂдсѓѓУЅ»сЂёсЂДсЂѓсѓЇсЂєсђѓт»Йт┐юсЂЎсѓІуиџтъІжЃетѕєуЕ║жќЊ
сЂ«сЂЊсЂесѓњ
уЏ┤С║цт░ётй▒Сйюућеу┤асЂеУеђсЂБсЂдсѓѓУЅ»сЂёсЂДсЂѓсѓЇсЂєсђѓт»Йт┐юсЂЎсѓІуиџтъІжЃетѕєуЕ║жќЊ  сЂ»
сЂ»
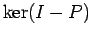 сЂеТЏИсЂЉсѓІсЂЊсЂесЂїтѕєсЂІсЂБсЂЪсЂїсђЂтЙїсЂ«сЂЪсѓЂсЂФсѓѓсЂєт░ЉсЂЌУф┐сЂ╣сЂдсЂісЂЊсЂєсђѓ
сЂеТЏИсЂЉсѓІсЂЊсЂесЂїтѕєсЂІсЂБсЂЪсЂїсђЂтЙїсЂ«сЂЪсѓЂсЂФсѓѓсЂєт░ЉсЂЌУф┐сЂ╣сЂдсЂісЂЊсЂєсђѓ
сЂЙсЂџ
ТўјсѓЅсЂІсЂФ
сЂДсЂѓсѓІсЂїсђЂ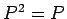 сѓѕсѓі
сѓѕсѓі
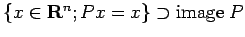 сѓѓтѕєсЂІ
сѓІсђѓт«ЪжџЏ
сѓѓтѕєсЂІ
сѓІсђѓт«ЪжџЏ
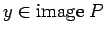 сЂесЂЎсѓІсЂесђЂ
сЂесЂЎсѓІсЂесђЂ
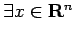 s.t.
s.t. 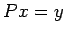 сЂесЂфсѓІсЂїсђЂ
сЂесЂфсѓІсЂїсђЂ
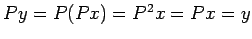 сЂДсЂѓсѓІсЂІсѓЅ
сЂДсЂѓсѓІсЂІсѓЅ
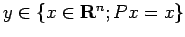 .
. 
- (1)
 сЂїтиЙуГЅсЂІсЂцт»ЙуД░сЂДсЂѓсѓІсЂЊсЂесЂ»у░АтЇўсЂфУеѕу«ЌсЂДтѕєсЂІсѓІсђѓ
сЂїтиЙуГЅсЂІсЂцт»ЙуД░сЂДсЂѓсѓІсЂЊсЂесЂ»у░АтЇўсЂфУеѕу«ЌсЂДтѕєсЂІсѓІсђѓ
- (2)
-
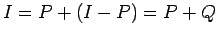 сЂДсЂѓсѓІсЂІсѓЅсђЂС╗╗ТёЈсЂ«
сЂДсЂѓсѓІсЂІсѓЅсђЂС╗╗ТёЈсЂ« 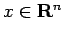 сЂФт»ЙсЂЌсЂд
сЂФт»ЙсЂЌсЂд
сѓєсЂѕсЂФ
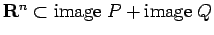 . сѓѓсЂАсѓЇсѓЊсЂЊсѓїсЂ»
уГЅтЈисЂФсЂфсѓІсђѓ
. сѓѓсЂАсѓЇсѓЊсЂЊсѓїсЂ»
уГЅтЈисЂФсЂфсѓІсђѓ
- (3)
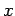 ,
, 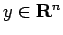 сЂесЂЎсѓІсЂесЂЇсђЂ
сЂесЂЎсѓІсЂесЂЇсђЂ
сЂДсЂѓсѓІсЂІсѓЅсђЂ
- (4)
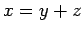 ,
,
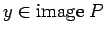 ,
,
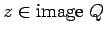 сЂесЂЌсѓѕсЂєсђѓ
сЂесЂЌсѓѕсЂєсђѓ
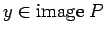 сѓѕсѓі
сѓѕсѓі 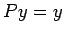 .
.
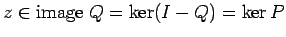 сѓѕсѓі
сѓѕсѓі 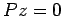 .
сѓєсЂѕсЂФ
.
сѓєсЂѕсЂФ
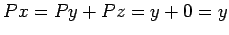 .
тљїТДўсЂФсЂЌсЂд
.
тљїТДўсЂФсЂЌсЂд
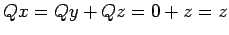 .
. 
ТАѓућ░ уЦљтЈ▓
2017-04-30
![\begin{jdefinition}[уЏ┤С║цт░ётй▒Сйюућеу┤а]
$V$\ сѓњ $\R^n$\ сЂ«уиџтъІжЃетѕєуЕ║ж...
...^n$\ сѓњ $V$\ сЂИсЂ«\textbf{уЏ┤С║цт░ётй▒Сйюућеу┤а}сЂетЉ╝сЂХсђѓ
\end{jdefinition}](img31.gif)
![\begin{jproposition}[уЏ┤С║цт░ётй▒Сйюућеу┤асЂ»тиЙуГЅсЂфт»ЙуД░уиџтйбСйюућеу┤а]
$\...
...2=P$.
\item $P$\ сЂ»т»ЙуД░сЂДсЂѓсѓІ: $P^T=P$.
\end{enumerate}\end{jproposition}](img32.gif)
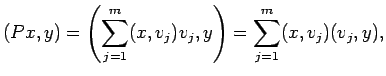
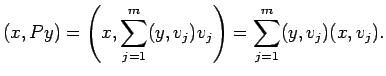
![]() ,
, ![]() сЂесЂёсЂєТЮАС╗ХсѓњТ║ђсЂЪсЂЎ
сЂесЂёсЂєТЮАС╗ХсѓњТ║ђсЂЪсЂЎ ![]() сЂ»жЂЕтйЊсЂфуиџтъІжЃетѕєуЕ║жќЊ
сЂ»жЂЕтйЊсЂфуиџтъІжЃетѕєуЕ║жќЊ ![]() сЂИсЂ«уЏ┤С║цт░ётй▒Сйюућеу┤асЂФсЂфсѓІсђѓ
сЂИсЂ«уЏ┤С║цт░ётй▒Сйюућеу┤асЂФсЂфсѓІсђѓ
![\begin{jproposition}[]
$P\in\R^{n\times n}$\ сЂї $P^2=P$, $P^T=P$\ сѓњТ║ђсЂЪсЂЎ...
...ІсЂесђЂ
$V$\ сЂИсЂ«уЏ┤С║цт░ётй▒Сйюућеу┤асЂ» $P$\ сЂФсЂфсѓІсђѓ
\end{jproposition}](img33.gif)
![]() ,
, ![]() сѓњТ║ђсЂЪсЂЎ
сѓњТ║ђсЂЪсЂЎ
![]() сЂ«сЂЊсЂесѓњ
уЏ┤С║цт░ётй▒Сйюућеу┤асЂеУеђсЂБсЂдсѓѓУЅ»сЂёсЂДсЂѓсѓЇсЂєсђѓт»Йт┐юсЂЎсѓІуиџтъІжЃетѕєуЕ║жќЊ
сЂ«сЂЊсЂесѓњ
уЏ┤С║цт░ётй▒Сйюућеу┤асЂеУеђсЂБсЂдсѓѓУЅ»сЂёсЂДсЂѓсѓЇсЂєсђѓт»Йт┐юсЂЎсѓІуиџтъІжЃетѕєуЕ║жќЊ ![]() сЂ»
сЂ»
![]() сЂеТЏИсЂЉсѓІсЂЊсЂесЂїтѕєсЂІсЂБсЂЪсЂїсђЂтЙїсЂ«сЂЪсѓЂсЂФсѓѓсЂєт░ЉсЂЌУф┐сЂ╣сЂдсЂісЂЊсЂєсђѓ
сЂеТЏИсЂЉсѓІсЂЊсЂесЂїтѕєсЂІсЂБсЂЪсЂїсђЂтЙїсЂ«сЂЪсѓЂсЂФсѓѓсЂєт░ЉсЂЌУф┐сЂ╣сЂдсЂісЂЊсЂєсђѓ![\begin{jproposition}[]
$P\in\R^{n\times n}$\ сЂїуЏ┤С║цт░ётй▒Сйюућеу┤асЂДсЂѓсѓІс...
...сЂфсЂБсЂЪсЂесЂЎсѓІсЂесђЂт«ЪсЂ» $y=Px$, $z=Qx$.
\end{enumerate}\end{jproposition}](img35.gif)