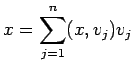懸案の問題を片付けよう。
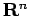 の基底
の基底 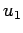 ,
, 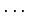 ,
, 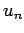 を、最初の
を、最初の 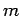 個
個
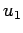 ,
,  ,
, 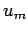 が
が 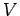 の基底になるように取る。
これに Gram-Schmidt の正規直交化を施して、
正規直交基底
の基底になるように取る。
これに Gram-Schmidt の正規直交化を施して、
正規直交基底 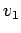 ,
,  ,
, 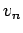 を作ると、
を作ると、
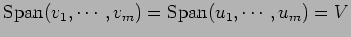 であるから、
であるから、 ,
,  ,
, 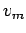 は
は
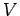 の正規直交基底になる。このとき実は
の正規直交基底になる。このとき実は
となることはほぼ明らかである。実際、任意の 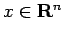 は
は
と展開できるが、
であるので、
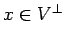 ならば
ならば
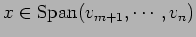 .
つまり
.
つまり
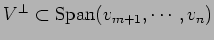 .
逆の
.
逆の
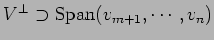 も簡単。
も簡単。
これで懸案だった
|
(2.4) |
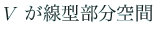 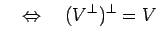 |
の証明が完結する。妙にてこずったように思われるかもしれないが、
実は無限次元の内積空間の場合には、
(5.3) は一般には成り立たない事実なのである。
桂田 祐史
2017-04-30