8.3 完全楕円積分

前項で $k\upto 1$ のとき、$F(1;k)$ が大きくなるのを見た。 実は完全楕円積分

$$K(k):=F(1;k)=\int_0^1\frac{\D t}{\sqrt{(1-t^2)(1-k^2t^2)}},$$

$$E(k):=E(1;k)=\int_0^1\sqrt{\frac{1-k^2t^2}{1-t^2}}\D t$$

について、以下が成り立つ。

$$K(0)=\pi/2, \quad E(0)=\pi/2,$$

$$k_1< k_2\quad\THEN\quad K(k_1)<K(k_2)\land E(k_1)>E(k_2),$$

$$\lim_{k\to 1-0}K(k)=\infty,\quad \lim_{k\to 1-0}E(k)=1$$

が成り立つ。

/*
 *
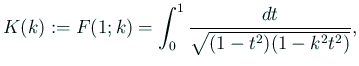 * g++ -I /opt/local/include testcomp.cpp
 */

#include <iostream>
#include <iomanip>
using namespace std;

#include <boost/math/special_functions/ellint_1.hpp>
#include <boost/math/special_functions/ellint_2.hpp>

int main(void)
{
  int i, n;
  double k, dk;
  n = 1000;
  dk = 1.0 / n;
  cout << setiosflags(ios::scientific) << setprecision(16);
  for (i = 0; i < n; i++) {
    k = min(1.0, i * dk);
    cout << k << " " << boost::math::ellint_1(k) << " "
	 << boost::math::ellint_2(k) << " " << endl;
  }
  return 0;
}

図 24: 第1種完全楕円積分 $K(k)$, 第2種完全楕円積分 $E(k)$

          k                    K(k)
  0.9000000000000000   2.2805491384227703
  0.9900000000000000   3.3566005233611920
  0.9990000000000000   4.4955963958421439
  0.9999000000000000   5.6451482168297478
  0.9999900000000000   6.7962149844353306
  0.9999990000000000   7.9474797735479656
  0.9999999000000001   9.0987690265206513
  0.9999999899999999  10.2500611890544686
  0.9999999990000000  11.4013537088987125
  0.9999999999000000  12.5526461950175943
  0.9999999999900000  13.7039387410005045
  0.9999999999990000  14.8552423897935242
  0.9999999999999000  16.0063684268750492
  0.9999999999999900  17.1582162205134168
  0.9999999999999990  18.3095087670103673
  0.9999999999999999  19.4081210556784711