Next: 5 一般の楕円関数と Weierstrassの楕円関数 Up: 4 AGM Previous: 4.2 不完全楕円積分の計算
![]() ,
, ![]() とする。
とする。
(20), (21) で数列 ![]() ,
,
![]() ,
, ![]() を求め、
を求め、
![]() が無視可能なくらい、
が無視可能なくらい、![]() を十分大きく取ったとする。
を十分大きく取ったとする。

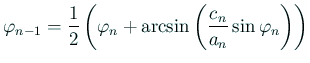

/*
* agm.cpp --- 算術幾何平均アルゴリズムによる K(k), sn(u;k), cn(u;k), dn(u;k)
* boost で計算したものと並べて表示させる。
*/
#include <iostream>
#include <cmath>
#include "easy_elliptic.hpp" // boost の楕円積分・楕円関数を簡単に使う
using namespace std;
int main(void)
{
int n, maxn = 20, N;
double k, kp, a[maxn+1], b[maxn+1], c[maxn+1], phi[maxn+1], eps, pi;
double u;
cout << setprecision(16);
pi = 4.0 * atan(1.0);
cout << "k="; cin >> k;
cout << "u="; cin >> u;
// AGM
eps = 1e-15;
kp = sqrt(1 - k * k);
a[0] = 1.0; b[0] = kp; c[0] = k;
cout << "k'=" << kp << endl;
for (n = 1; n < maxn; n++) {
a[n] = (a[n-1] + b[n-1]) / 2;
b[n] = sqrt(a[n-1] * b[n-1]);
c[n] = (a[n-1] - b[n-1]) / 2;
if (c[n] < eps * a[n]) {
cout << "ite=" << n << ", a_n=" << a[n] << ", b_n=" << b[n] << endl;
break;
}
}
N = n;
// 完全楕円積分
cout << "k=" << k << endl;
cout << "K(k)=" << K(k) << ", " << pi / (2 * a[N]) << endl;
// 不完全楕円積分
// 楕円関数
phi[N] = (1 << n) * a[N] * u; // φN
for (n = N; n >= 1; n--)
phi[n-1] = (phi[n] + asin(c[n] * sin(phi[n]) / a[n])) / 2;
cout << "u=" << u << endl;
cout << "sn(u;k)=" << sn(k,u) << ", " << sin(phi[0]) << endl;
cout << "cn(u;k)=" << cn(k,u) << ", " << cos(phi[0]) << endl;
cout << "dn(u;k)=" << dn(k,u) << ", " << cos(phi[0]) / cos(phi[1]-phi[0])
<< endl;
return 0;
}