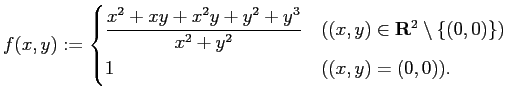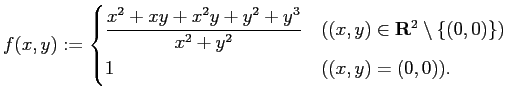

Next: D..2.1 Mathematicaでやってみる
Up: D. Mathematicaの多変数の微積分への応用
Previous: D..1 はじめに
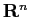 の開集合
の開集合 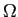 で定義された関数
で定義された関数
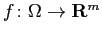 について、
(a)
について、
(a) 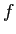 は連続,
(b)
は連続,
(b) 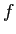 は各変数につき偏微分可能,
(c)
は各変数につき偏微分可能,
(c) 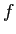 は
は 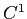 級,
(d)
級,
(d) 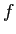 は全微分可能,
という4つの条件を考える。
は全微分可能,
という4つの条件を考える。
- (1)
- 条件 (d) が成り立つとはどういうことか定義を述べよ。
- (2)
- 条件 (a), (b), (c), (d) 間の関係について説明せよ。
- (3)
- 次式で定義される
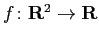 について以下の (i), (ii) に答えよ。
(i)
について以下の (i), (ii) に答えよ。
(i)
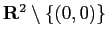 で
で 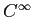 級であることを示せ。
(ii)
級であることを示せ。
(ii) 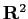 で条件 (a), (b), (c), (d) を満たすかどうか調べよ。
で条件 (a), (b), (c), (d) を満たすかどうか調べよ。
Subsections


Next: D..2.1 Mathematicaでやってみる
Up: D. Mathematicaの多変数の微積分への応用
Previous: D..1 はじめに
桂田 祐史
2013-04-09