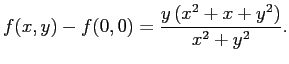
In[1] := f[x_,y_]:=(x^2+x y+x^2 y+y^2+y^3)/(x^2+y^2) In[2] := f[0,0]=1 In[3] := Simplify[f[x,y]-f[0,0]] |
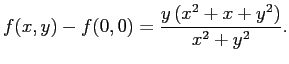
分子の高次の項を無視すると
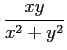 に等しく、
分母分子ともに
に等しく、
分母分子ともに
In[4] := % /. y-> m x In[5] := Limit[%, x->0] |
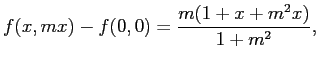
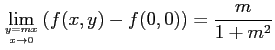
が得られる。この結果は
ゆえに
次に ![]() での偏微分可能性を調べる。
での偏微分可能性を調べる。
In[6] := Simplify[(f[h,0]-f[0,0])/h] In[7] := Simplify[(f[0,h]-f[0,0])/h] |
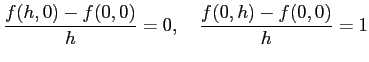
が得られる。ゆえに (Limit[%,h->0] とするまでもなく)
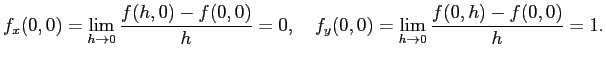
ゆえに