A..1 $\arctan$ の Taylor 展開を用いて計算する

既に言ってあるように、

http://nalab.mind.meiji.ac.jp/~mk/syori2-2012/jouhousyori2-2012-06/node7.html

で紹介した piarctan.BAS が叩き台になる。 これは、与えられた $x$ , $N$ に対して、 級数

$$\tan^{-1} x=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{2n-1}x^{2n-1}$$ (1)

の第 $N$ 部分和 $S_N$ を計算するプログラムである。

piarctan.BAS (再掲)

REM piarctan.BAS --- マーダヴァ・グレゴリー・ライプニッツ級数でπを計算
REM arctan x の級数を第 n 項まで計算
INPUT X
INPUT N
F=-X*X
T=X
S=0
FOR J=1 TO N
  A=T/(2*J-1)
  S=S+A
  T=F*T
NEXT J
PRINT "arctan(x)≒";S
PRINT "その4倍";4*S
REM 組込み定数 PI との差を計算してみる
PRINT USING "πとの差=-%.###^^^^^^";4*S-PI
END

$x=1$ の場合の

$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$

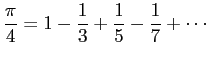
は有名であるが、収束は非常に遅い。実際、実験で見た通り、

$$\pi-4S_N\kinji \frac{1}{N}$$

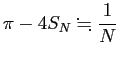
が成り立つ (1億($=10^8$ )項足して、誤差 $10^{-8}$ -- $10$ 桁も合わない)。 どんなにコンピューターが速くても、 $100$ 桁の精度の値を計算するのは無理である。

しかし、これは $x$ の値として、収束ギリギリの $x=1$ を代入するからである (実際、(1) の収束半径は $1$ である, 冪級数は収束円の内部では必ず収束するが円周上の点で収束するかどうかは case by case で収束しても「遅い」場合が多い)。 $\vert x\vert<1$ なる $x$ に対しては、 (1) の収束はぐっと速くなる。

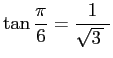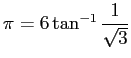一番簡単なのは、高校生も知っている $\tan\dfrac{\pi}{6}=\dfrac{1}{\sqrt{3 }\;}$ に基づく、 $\pi=6\tan^{-1}\dfrac{1}{\sqrt{3}}$ を用いることである。

INPUT X を X=1/SQR(3) に変え、 $4$ をかけるところを $6$ をかけるように変えたものが次のプログラムである (OPTION ARITHMETIC DECIMAL_HIGH にも変えた)。

kadai6b1.BAS

REM kadai6b1.BAS --- マーダヴァ・グレゴリー・ライプニッツ級数でπを計算
REM arctan(1/√3) の級数を第N項まで計算
OPTION ARITHMETIC decimal_high
INPUT N
LET X=1/SQR(3)
LET F=-X*X
LET T=X
LET S=0
FOR J=1 TO N
   LET A=T/(2*J-1)
   LET S=S+A
   LET T=F*T
NEXT J
PRINT "6*arctan(x)≒";6*S
REM 組込み定数 PI との差を計算してみる
PRINT USING "πとの差=-%.###^^^^^^":6*S-PI
END

最後に PI と比較しているのは、 カンニングであるが (苦笑)、 その結果は次のようになり、 $N=210$ くらいで $100$ 桁精度を実現しているようである (差が大体 $3.9\times10^{-103}$ であるから)。

kadai6b1.TXT ($N=210$ の場合)

? 210
6*arctan(x)≒ 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798175415515142074668914143478172519579252999001468666117910963800249473594922589558451149412426597243798192135258779349163444188419002776980473968671998254815310845772183661993477117122206330295980300468265032425044971769581966122368923975830190359265260280452439469056239411353322600285365354079198623561329837112540037802583883742612430308012431266108485579200748300447615517051621776071743812297241593061362796460193924590409288715907812776745710640173447366147858476628929330128224069043383756471261001339104089689573643179485746003276589222538648739794448220503879861605852796470434461563725003377966770398821962936563887508996436649003257909678486654464777327912490175223366294675627953729664047127912971230253567836505483256602936448002590856734658997052628800136082809703995747012631975584920533663300884564944271834022542189687366731857503436221868148525708031224234008111518938525225632668655196746 
πとの差=-3.939E-0103

$N$ が増加するにつれて、精度がどのように上がっていくか見るために、 INPUT N をやめて、 全体を

FOR N=10 TO 210 STEP 10
...
NEXT N

と FOR NEXT ループにして、次の表 2 の結果を得る。

図 2: 項数 $N$ と誤差

$N$	誤差
$10$	$-2.143\times 10^{-6}$
$20$	$-1.839\times 10^{-11}$
$30$	$-2.085\times 10^{-16}$
$40$	$-2.654\times 10^{-21}$
$50$	$-3.601\times 10^{-26}$
$60$	$-5.086\times 10^{-31}$
$70$	$-7.387\times 10^{-36}$
$80$	$-1.095\times 10^{-40}$
$90$	$-1.649\times 10^{-45}$
$100$	$-2.514\times 10^{-50}$
$110$	$-3.872\times 10^{-55}$
$120$	$-6.011\times 10^{-60}$
$130$	$-9.399\times 10^{-65}$
$140$	$-1.478\times 10^{-69}$
$150$	$-2.337\times 10^{-74}$
$160$	$-3.710\times 10^{-79}$
$170$	$-5.915\times 10^{-84}$
$180$	$-9.461\times 10^{-89}$
$190$	$-1.518\times 10^{-93}$
$200$	$-2.442\times 10^{-98}$
$210$	$-3.939\times 10^{-103}$

図 3: 項数 $N$ と誤差 (縦軸対数目盛)

誤差が大体等比数列的に ($N$ に関して指数関数的に？) 0 に収束している様子が 分かる 本当はこういうのはグラフにするのが良い。 ここでは gnuplot (1年生のときに習ったはず) を使ってみたが、 もちろん十進 BASIC で描くのも簡単である。

それでは、要求されていた結果を求めるプログラムを作ろう。 課題2Bでやったように、FOR NEXT で N を大きくして行って、 部分和を計算するプログラムにする。

kadai6b2.BAS

REM kadai6b2.BAS --- マーダヴァ・グレゴリー・ライプニッツ級数でπを計算
REM arctan(1/√3) の級数を10,20,...,250項まで計算
REM 結果は小数点以下110位まで表示
OPTION ARITHMETIC decimal_high
LET FMT$="N=### -%."&REPEAT$("#",110)
LET N=250
LET X=1/SQR(3)
LET F=-X*X
LET T=X
LET S=0
FOR J=1 TO N
   LET A=T/(2*J-1)
   LET S=S+A
   LET T=F*T
   IF MOD(J , 10) =0 THEN
      PRINT USING fmt$:J,6*S
   END IF
NEXT J
REM 組込み定数 PI との差を計算してみる
PRINT USING "πとの差=-%.###^^^^^^":PI-6*S
END

結果は次のようになる (TEX で \scriptsize コマンドを使って縮小)。

N= 10  3.14159051093808009964275422994425504368823543729459863385301608264097243139275244243408049537664837144194195965
N= 20  3.14159265357140338177371056457791845749708370902558800062450336039110974863967354187227900363909324495379551167
N= 30  3.14159265358979302993126907675698512128890364163387594078160677223250316907504141910094384327780556430672531665
N= 40  3.14159265358979323845998904545815723164682333580898559851810755021711576515774234507828600074005410050567590231
N= 50  3.14159265358979323846264334727215223712766242383933328994947074253583407491260142245980404128750279799354137185
N= 60  3.14159265358979323846264338327899429478611788675967126248193958028428440424653148715465478961463146251880103922
N= 70  3.14159265358979323846264338327950287681011408881114209344980232821142119403271477392517560945005206755050370174
N= 80  3.14159265358979323846264338327950288419705988682105507083891588023987499387955321296887381276928532730590072263
N= 90  3.14159265358979323846264338327950288419716939772598750958858556364736336671762754275139106652717651497248200692
N=100  3.14159265358979323846264338327950288419716939937508067873446993355312916323675359893283010326258393751533470850
N=110  3.14159265358979323846264338327950288419716939937510582058777735023191320405347993715459391151728912750033891584
N=120  3.14159265358979323846264338327950288419716939937510582097493858083854337957828522717360102517299756190923350247
N=130  3.14159265358979323846264338327950288419716939937510582097494459221382757184428319165349115190289161510116917782
N=140  3.14159265358979323846264338327950288419716939937510582097494459230781492806566013451682112808110943615477604646
N=150  3.14159265358979323846264338327950288419716939937510582097494459230781640626284131806763014633707611386690905481
N=160  3.14159265358979323846264338327950288419716939937510582097494459230781640628620862758871391779973144580812870063
N=170  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862212031675396342638517754282
N=180  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803473073620684479093638320
N=190  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534059912106400090011
N=200  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211704355929502943
N=210  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798175415515
N=220  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808014
N=230  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651
N=240  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651
N=250  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651
πとの差= 2.722E-0122

少々字が小さくて見づらいが、 $N=230,240,250$ の場合に、 小数点以下$110$ 位までの小数表示が一致していることが分かる。 これで小数点以下$100$ 位までの値は得られていると考えて良いだろう。

円周率 $\pi$ の小数点以下 $110$ 位まで

 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510
   58209 74944 59230 78164 06286 20899 86280 34825 34211 70679
   82148 08651

(要求されていたのは、$100$ 位までだったが、$101$ 位が `8' で、 四捨五入を考えると微妙なので、$110$ 位まで表示しておく。)

100桁の数をそのまま表示されても読みづらいので、 10あるいは5桁ごとにブランクをいれるなどすると親切であろう。 なお、筆者自身はそれを「手で」行ったが、 過去に十進 BASIC にやらせた学生もいた (感心しました)。

(参考) pi100.BAS 5桁ずつ区切って表示

OPTION ARITHMETIC decimal_high
LET FMT$="%."&REPEAT$("#",110)
LET PI100$=USING$(fmt$,PI)
PRINT "3."
FOR i=0 TO 20
   PRINT mid$(PI100$,i*5+3,5)&" ";
   IF MOD(i,10)=9 THEN
      PRINT
   END if
NEXT i
END

pi100.TXT

3.
14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 
58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 
82148