

Next: A..1 の Taylor 展開を用いて計算する
Up: 情報処理2 第9回 Mathematica 体験
Previous: 5 レポート課題10(案)
課題6B
「円周率計算の歴史」
で書いたように、円周率 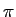 の効率的な計算法には、
(i)
の効率的な計算法には、
(i)
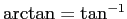 のような逆三角関数の Taylor 展開を利用する方法,
(ii) AGM 公式を利用する方法,
(iii) ラマヌジャンの公式 (またはその系列) を利用する方法, などがある。
のような逆三角関数の Taylor 展開を利用する方法,
(ii) AGM 公式を利用する方法,
(iii) ラマヌジャンの公式 (またはその系列) を利用する方法, などがある。
ここでは、主に単純な (i) の方法を解説する。
Subsections


Next: A..1 の Taylor 展開を用いて計算する
Up: 情報処理2 第9回 Mathematica 体験
Previous: 5 レポート課題10(案)
桂田 祐史
2012-06-27
![]() の効率的な計算法には、
(i)
の効率的な計算法には、
(i)
![]() のような逆三角関数の Taylor 展開を利用する方法,
(ii) AGM 公式を利用する方法,
(iii) ラマヌジャンの公式 (またはその系列) を利用する方法, などがある。
のような逆三角関数の Taylor 展開を利用する方法,
(ii) AGM 公式を利用する方法,
(iii) ラマヌジャンの公式 (またはその系列) を利用する方法, などがある。