

Next: 2.2 �$BB?9`<0�(B (�$B$^$?$O�(B )
Up: 2 �$BHsF1
Previous: 2 �$BHsF1
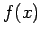 �$B$,B?9`<0$J$i$P!"�(B
�$B$,B?9`<0$J$i$P!"�(B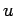 �$B$OB?9`<0$G5a$^$k!#�(B
�$B$OB?9`<0$G5a$^$k!#�(B
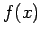 �$B$,�(B
�$B$,�(B 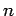 �$B �$B$b�(B
�$B �$B$b�(B 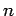 �$B �$B$h$jBg$-$/$7$J$$$H5a$^$i$J$$$3$H$,$"$k!#�(B
�$B>\$7$/$O�(B
�$B �$B$h$jBg$-$/$7$J$$$H5a$^$i$J$$$3$H$,$"$k!#�(B
�$B>\$7$/$O�(B
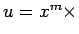 �$BF1$8 �$B$O$"$k�(B 0 �$B0J>e$N@0?t�(B)�$B!#�(B
�$BF1$8 �$B$O$"$k�(B 0 �$B0J>e$N@0?t�(B)�$B!#�(B
�$B;n$7$K!"�(B(i)
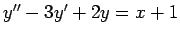 , (ii)
, (ii)
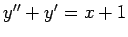 ,
(iii)
,
(iii) 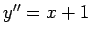 �$B$r2r$$$F$_$h$&!#�(B
�$B$r2r$$$F$_$h$&!#�(B
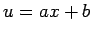 (
(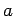 ,
, 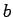 �$B$OL$Dj78?t�(B) �$B$HCV$$$FBeF~$9$k$H!D�(B
�$B$OL$Dj78?t�(B) �$B$HCV$$$FBeF~$9$k$H!D�(B
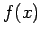 �$B$,�(B
�$B$,�(B
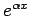 �$B$J$i$P!"�(B
�$B$J$i$P!"�(B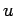 �$B$b�(B
�$B$b�(B
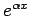 �$B$NDj?tG\$G5a$^$k�(B
-- �$B$H8@$$$?$$$,!"�(B
�$B$3$l$O$D$M$K@5$7$$Lu$G$O$J$$!#�(B
�$B$NDj?tG\$G5a$^$k�(B
-- �$B$H8@$$$?$$$,!"�(B
�$B$3$l$O$D$M$K@5$7$$Lu$G$O$J$$!#�(B
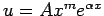 �$B$H$9$kI,MW$,$"$k$H$-$b$"$k�(B (
�$B$H$9$kI,MW$,$"$k$H$-$b$"$k�(B (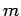 �$B$O$"$k�(B 0 �$B0J>e$N@0?t�(B)�$B!#�(B
�$B$O$"$k�(B 0 �$B0J>e$N@0?t�(B)�$B!#�(B
�$B;n$7$K�(B (iv)
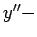
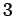
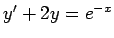 ,
(v)
,
(v)
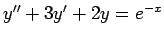 , (vi)
, (vi)
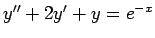 �$B$r2r$$$F$_$h$&!#�(B
�$B$r2r$$$F$_$h$&!#�(B
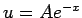 �$B$HCV$$$FBeF~$9$k$H!D�(B
�$B$HCV$$$FBeF~$9$k$H!D�(B
- �$B0lHL$K�(B
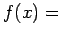 �$BB?9`<0�(B
�$BB?9`<0�(B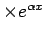 �$B$N�(B
�$BFC2r$O�(B
�$B$N�(B
�$BFC2r$O�(B
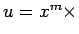 �$BF1$8 �$B$N7A$G5a$^$k�(B
(
�$BF1$8 �$B$N7A$G5a$^$k�(B
(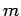 �$B$O$"$k�(B 0 �$B0J>e$N@0?t�(B)�$B!#�(B
�$B$O$"$k�(B 0 �$B0J>e$N@0?t�(B)�$B!#�(B


Next: 2.2 �$BB?9`<0�(B (�$B$^$?$O�(B )
Up: 2 �$BHsF1
Previous: 2 �$BHsF1
Masashi Katsurada
�$BJ?@.�(B20�$BG/�(B1�$B7n�(B10�$BF|�(B