Next: B. 束 Up: 1年生向け確率論ノート Previous: 13 余談: 熱方程式、拡散方程式の基本解
G. Boole が論理計算の場として導入したものであるが、 論理以外にも可測集合族などの集合束としてあちこちに現れる。
集合 ![]() が与えられ、その任意の 2 要素
が与えられ、その任意の 2 要素 ![]() ,
, ![]() に対して
に対して ![]() ,
,
![]() と書かれる
と書かれる ![]() の元が対応づけられていて、次の法則が成り立つ
ものとする。
の元が対応づけられていて、次の法則が成り立つ
ものとする。
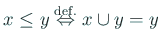
なお、![]() に対して
に対して ![]() は一意に定まり、
は一意に定まり、
![]() の補元 (complement) と呼ばれる。
の補元 (complement) と呼ばれる。
![]() ,
, ![]() ,
, ![]() を Boole 演算と総称する。
を Boole 演算と総称する。
これに関して De Morgan の法則 (De Morgan's law)