離散的確率変数 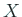 が取り得る値が
が取り得る値が 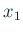 ,
, 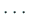 ,
, 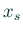 で、
で、
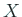 の確率分布が
の確率分布が
で与えられているとき
で定まる 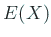 を確率変数
を確率変数 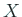 のきたいち期待値
(expectation) あるいは
平均 (mean) と呼ぶ。また、
のきたいち期待値
(expectation) あるいは
平均 (mean) と呼ぶ。また、
で定まる 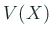 を確率変数
を確率変数 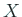 のぶんさん
分散 (variance) と呼ぶ。
のぶんさん
分散 (variance) と呼ぶ。
分散はつねに 0 以上の値を取る。
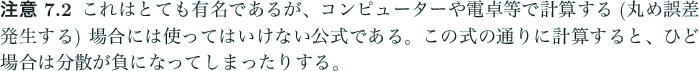

平均から離れる確率はあまり大きくなれない、
ということを表わしている式である。
しかし、この式は理論上活躍することは多いが、
実際の問題に直接役立つことはない。
桂田 祐史
![]() が取り得る値が
が取り得る値が ![]() ,
, ![]() ,
, ![]() で、
で、
![]() の確率分布が
の確率分布が
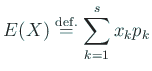
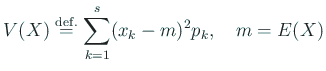
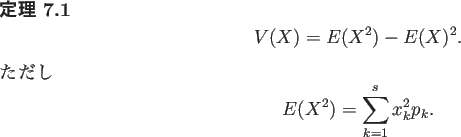
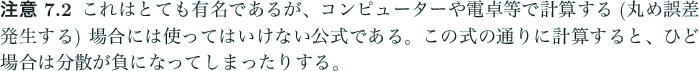
![\begin{jdefinition}[確率変数の標準偏差]\upshape
確率変数 $X$ の�...
...\sqrt{V(X)}=\sqrt{\sum_{k=1}^s (x_k-m)^2p_k}.
\end{displaymath}\end{jdefinition}](img126.gif)

![\begin{jtheorem}[チェビシェフ (Cebysev) の不等式]\upshape
\index{ち�...
...\vert X-m\vert\ge \lambda\sigma)\le 1/\lambda^2.
\end{displaymath}\end{jtheorem}](img128.gif)