Next: 4.0.0.1 証明 Up: 1年生向け確率論ノート Previous: 3.0.0.4 証明
![]() ,
, ![]() を事象とする。
を事象とする。![]() が起こったことが分かったが、
が起こったことが分かったが、![]() が起こっ
たかどうか分からないという状況で、
が起こっ
たかどうか分からないという状況で、![]() の起こりやすさを示す度合 -- 事
象
の起こりやすさを示す度合 -- 事
象 ![]() のもとでの事象
のもとでの事象 ![]() の条件つき確率
の条件つき確率 ![]() -- を導入する。
-- を導入する。

上の例題では、
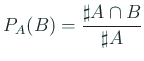
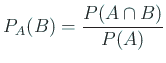
![]()

|
条件つき確率 ![]() は
は ![]() と等しくなることも、等しくならないこ
ともある (例題2, 例3)。
と等しくなることも、等しくならないこ
ともある (例題2, 例3)。

|
|
|