Next: 1 おまけ Mathematica Up: 1 Mathematica で Fourier級数 Previous: 3 細かい工夫 周期関数の定義
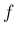 の Fourier 係数
の Fourier 係数
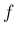 の Fourier 級数展開を求めてみよう。
の Fourier 級数展開を求めてみよう。
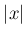 は偶関数であるから、
は偶関数であるから、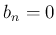 はすぐ分かる
(実際、
はすぐ分かる
(実際、
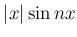 は奇関数であるから
は奇関数であるから
![$[-\pi,\pi]$](img50.png) で積分すると 0)。
で積分すると 0)。
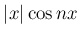 は偶関数で、
は偶関数で、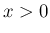 では
では 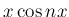 に等しいので、
に等しいので、
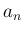 |
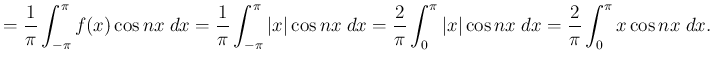 |
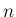 の値で場合分けが必要である。
の値で場合分けが必要である。
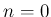 のときは、
のときは、
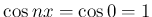 であるから
であるから
![$\displaystyle a_0=\frac{2}{\pi}\int_0^\pi x\;\Dx
=\frac{2}{\pi}\cdot\left[\frac{x^2}{2}\right]_0^\pi=\pi.
$](img76.png)
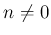 のときは
のときは
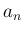 |
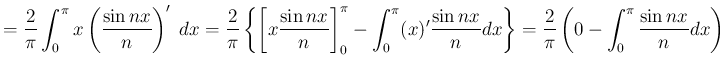 |
||
![\begin{align*}=\frac{2}{\pi}\left[\frac{\cos nx}{n^2}\right]_{0}^\pi
=\frac{2}{n...
... \text{($n$\ は奇数)} \\ [1ex]
0& \text{($n$\ は偶数)}.
\end{array}\right.\end{align*}](img78.png) |
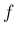 の Fourier級数は
の Fourier級数は
=\frac{\pi}{2}
-\sum_{n\ge 1\atop \text{$n$は偶数}}\dfrac{4}...
...t(\frac{\cos x}{1^2}+\frac{\cos
3x}{3^2}
+\frac{\cos 5x}{5^2}+\cdots\right).
$](img79.png)