Next: 5 次元における Laplacian の差分近似 Up: 4 Laplacian の極座標表示 Previous: 3次元の極座標変換を2つの3次元円柱座標変換に分解する方法
グリーンの公式を用いると、
ラプラシアンは 1 階微分である ![]() で特徴づけることができる。
重積分の極座標への変数変換の公式、
変分法の基本補題を放り込めば問題が解決できる。
-- このやり方は結構あちこちに載っているが、それほど簡単とは言えない。
しかし、
より複雑な座標変換を用いる場合への一般化が期待できるという点に価値がある
(と筆者には想像される -- 正直言うとよく知らない)。
で特徴づけることができる。
重積分の極座標への変数変換の公式、
変分法の基本補題を放り込めば問題が解決できる。
-- このやり方は結構あちこちに載っているが、それほど簡単とは言えない。
しかし、
より複雑な座標変換を用いる場合への一般化が期待できるという点に価値がある
(と筆者には想像される -- 正直言うとよく知らない)。
まず ![]() の極座標による
の極座標による ![]() の内積の公式を導く。
の内積の公式を導く。
|
|
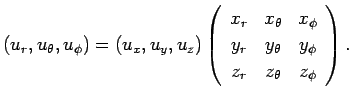
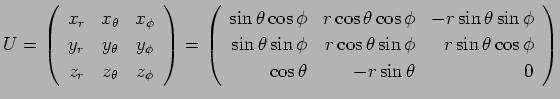
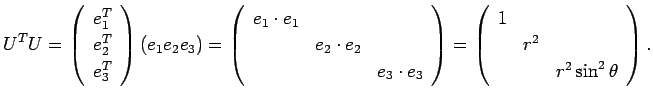
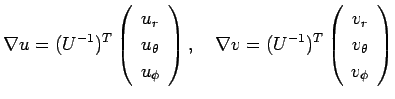
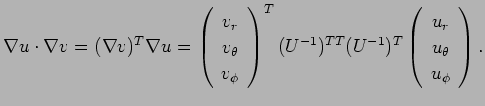
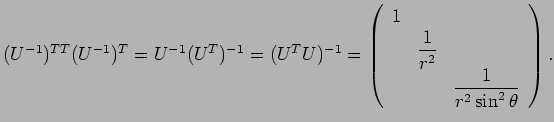
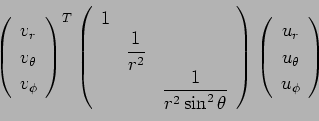 |
|||
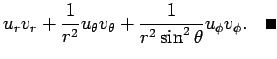 |
さて、![]() を
を ![]() (on
(on ![]() ) を満たす関数とすると、
Green の定理から
) を満たす関数とすると、
Green の定理から
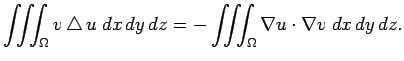
![]() を極座標表示した式
(6) を代入して
を極座標表示した式
(6) を代入して
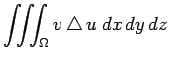 |
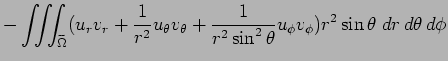 |
||
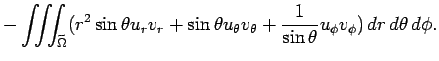 |
部分積分を施し、積分変数を元に戻すと
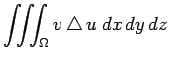 |
![$\displaystyle = \tint_{\widetilde\Omega} \left[ \frac{\rd}{\rd r}(r^2\sin\theta...
...\phi}\left(\frac{1}{\sin\theta}u_\phi\right) \right] v \D r \D\theta \D\phi$](img169.png) |
|
![$\displaystyle = \tint_\Omega\frac{1}{r^2\sin\theta}\left[ \frac{\rd}{\rd r}(r^2...
...\frac{\rd}{\rd\phi} \left(\frac{1}{\sin\theta}u_\phi\right)\right] v \DxDyDz.$](img170.png) |
![]() の任意性から (変分法の基本補題から、というべきか)
の任意性から (変分法の基本補題から、というべきか)
![$\displaystyle \Laplacian u
= \frac{1}{r^2\sin\theta}\left[
\frac{\rd}{\rd r}(r^...
...u_\theta)
+\frac{\rd}{\rd\phi}
\left(\frac{1}{\sin\theta}u_\phi\right)\right].
$](img171.png)
![$\displaystyle \Laplacian u
= \frac{\rd^2 u}{\rd r^2}+\frac{2}{r}\frac{\rd u}{\r...
...ta}\right)
+\frac{1}{\sin^2\theta}\frac{\rd^2 u}{\rd\phi^2}
\right]. \quad\qed
$](img172.png)
![]() における
における
![]() の極座標表示については、
の極座標表示については、
桂田 祐史