3次元の極座標変換を2つの3次元円柱座標変換に分解する方法

まずは私のお勧めの方法から紹介しよう。 これは3次元の極座標変換の、2つの3次元円柱座標変換への分解に基づくもので、 計算は比較的シンプルで済み (要するに面倒なことが全部2次元Laplacianの極座標表示に押し付けられている)、 高次元への一般化も可能という、 すぐれた方法である。 それにもかかわらず、案外載っている本が少ない (もちろん杉浦 [1] には載っている)。

$\rho=r\sin\theta$ とおくと、

$$\left\{ \begin{array}{l} x=\rho\cos\phi\\ y=\rho\sin\phi\\ z=z ... ...in{array}{l} z=r\cos\theta\\ \rho=r\sin\theta\\ \phi=\phi \end{array}\right.$$

であるから、

$$\frac{\rd^2}{\rd x^2}+\frac{\rd^2}{\rd y^2}%+\frac{\rd^2}{\rd z^2... ...rd}{\rd\rho} +\frac{1}{\rho^2}\frac{\rd^2}{\rd\phi^2}%+\frac{\rd^2}{\rd z^2} ,$$

$$\frac{\rd^2}{\rd\rho^2} +\frac{\rd^2}{\rd z^2} =\frac{\rd^2}{\rd r^2}+\frac{1}{r}\frac{\rd}{\rd r} +\frac{1}{r^2}\frac{\rd^2}{\rd\theta^2}.$$

辺々加えて

$$\frac{\rd^2}{\rd x^2}+\frac{\rd^2}{\rd y^2}+\frac{\rd^2}{\rd z^2}... ...rd}{\rd\rho} +\frac{1}{\rho^2}\frac{\rd^2}{\rd\phi^2}%+\frac{\rd^2}{\rd z^2} .$$

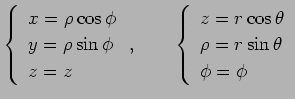
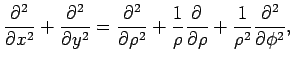
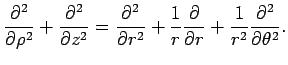
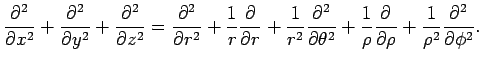
2次元極座標に関する

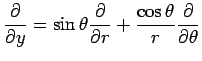
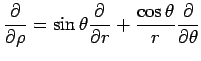
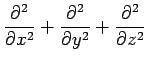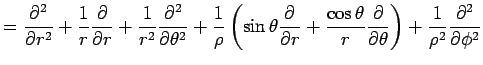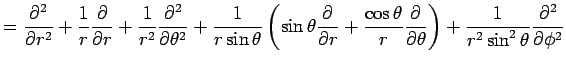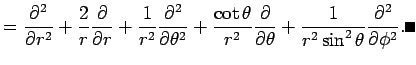$$\frac{\rd}{\rd y} =\sin\theta\frac{\rd}{\rd r}+\frac{\cos\theta}{r}\frac{\rd}{\rd\theta}$$

という公式と同様にして

$$\frac{\rd}{\rd\rho} =\sin\theta\frac{\rd}{\rd r}+\frac{\cos\theta}{r}\frac{\rd}{\rd\theta}$$

が得られる。ゆえに

$$\frac{\rd^2}{\rd x^2}+\frac{\rd^2}{\rd y^2}+\frac{\rd^2}{\rd z^2} =\frac{\rd^2}{\rd r^2}+\frac{1}{r}\frac{\rd}{\rd r} +\frac{1}{r^2... ...theta}{r}\frac{\rd}{\rd\theta} \right) +\frac{1}{\rho^2}\frac{\rd^2}{\rd\phi^2}$$

$$=\frac{\rd^2}{\rd r^2}+\frac{1}{r}\frac{\rd}{\rd r} +\frac{1}{r^2... ...\frac{\rd}{\rd\theta} \right) +\frac{1}{r^2\sin^2\theta}\frac{\rd^2}{\rd\phi^2}$$

$$=\frac{\rd^2}{\rd r^2}+\frac{2}{r}\frac{\rd}{\rd r} +\frac{1}{r^2... ...2}\frac{\rd}{\rd\theta} +\frac{1}{r^2\sin^2\theta}\frac{\rd^2}{\rd\phi^2}. \qed$$