1.0.0.1 蛇足的注意

プログラミング言語の C や Fortran には角度を計算するための関数 atan2() がある¹。 atan2(y,x) とすると、点 $(x,y)$ の角度を $[-\pi,\pi]$ の範囲で返す。 そこで C プログラムで $(x,y)$ から $(r,\theta)$ を計算するには

    r=sqrt(x*x+y*y)
    phi=atan2(y,x)
    if (phi < 0.0) then
      phi=phi+2*pi
    endif

    r = sqrt(x * x + y * y);
    theta = atan2(y, x);
    if (phi < 0.0) phi += 2 * pi;

とするとよい (もちろん pi には $\pi$ の値が入っているとしている)。 関数 atan2() を使わずに atan() のみで角度 $\theta$ を求め ようとすると、分かりにくいプログラムになる。 $\qedsymbol$

なお、

平面極座標のヤコビアン

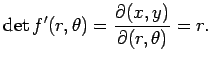
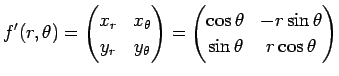
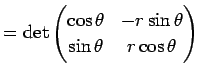$x=r\cos\theta$, $y=r\sin\theta$ により $f\colon(r,\theta)\mapsto (x,y)$ を定義すると

$$\det f'(r,\theta) =\frac{\rd(x,y)}{\rd(r,\theta)}=r.$$

証明. ヤコビ行列は

$$f'(r,\theta) =\left( \begin{matrix} x_r & x_\theta \\ y_r & y_\t... ...ix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \end{matrix}\right)$$

であるから、

$$\det f'(r,\theta) =\det \left( \begin{matrix}\cos\theta & -r\sin\theta \sin\theta & r\cos\theta \end{matrix} \right)$$

$$=\cos\theta\cdot r\cos\theta-(-r\sin\theta)\sin\theta =r(\cos^2\theta+\sin^2\theta)$$

$$=r. \qed$$

$\qedsymbol$