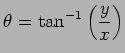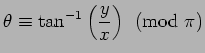平面に直交する座標軸 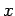 軸,
軸,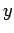 軸を取って座標を入れる
軸を取って座標を入れる 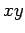 座標系で、
座標系で、
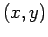 という座標を持つ点
という座標を持つ点
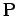 の原点
の原点
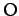 からの距離を
からの距離を 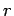 ,
,
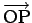 が
が 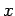 軸の正方向となす角を
軸の正方向となす角を 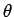 (
(
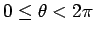 ) とすると、
) とすると、
がなりたつ。
写像
は 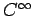 - 級で、定義域を
- 級で、定義域を 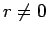 の範囲、すなわち
の範囲、すなわち
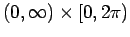 に制限すれば
に制限すれば 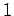 対
対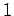 である。特に
である。特に
は全単射である。
逆の計算、つまり 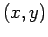 から
から
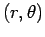 を求めるには、
を求めるには、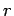 の方は
の方は
と 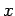 ,
, 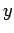 の式として簡単に表されるが、
の式として簡単に表されるが、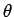 の方は標準的な
記法がない。強いて書けば
の方は標準的な
記法がない。強いて書けば
であろうか。多くの本に
とあるが、
これは色々と問題を含んでいる式である (はっきり言えば「マズイ」)。
実際、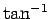 は
は
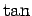 の逆関数であるが、これが主値を表すと解釈すると値の範囲が
の逆関数であるが、これが主値を表すと解釈すると値の範囲が
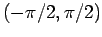 と幅
と幅 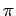 に制限されてしまう。この式だけでは
角度
に制限されてしまう。この式だけでは
角度 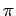 の差は無視されることになる。
そもそも
の差は無視されることになる。
そもそも
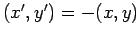 として定義した
として定義した 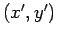 は、
は、
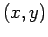 とは角度
とは角度 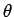 が
が 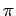 異なるはずであるが、
異なるはずであるが、
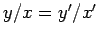 であるから、
であるから、
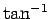 を施す以前に角度
を施す以前に角度 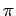 の違いが消えてしまう。
それ以外の情報 (
の違いが消えてしまう。
それ以外の情報 (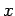 ,
, 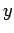 の符号など) から再生する手続きが必要になる。
の符号など) から再生する手続きが必要になる。
は正しい式であるのだが、これだけでは不十分であろう。
Subsections
桂田 祐史
![]() 軸,
軸,![]() 軸を取って座標を入れる
軸を取って座標を入れる ![]() 座標系で、
座標系で、
![]() という座標を持つ点
という座標を持つ点
![]() の原点
の原点
![]() からの距離を
からの距離を ![]() ,
,
![]() が
が ![]() 軸の正方向となす角を
軸の正方向となす角を ![]() (
(
![]() ) とすると、
) とすると、
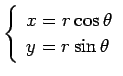
![]() から
から
![]() を求めるには、
を求めるには、![]() の方は
の方は