Next: 3 дёҖиҲ¬гҒ® гҒ«гҒҠгҒ‘гӮӢжҘөеә§жЁҷ Up: Laplacian гҒЁжҘөеә§жЁҷ Previous: 1.0.0.1 иӣҮи¶ізҡ„жіЁж„Ҹ
з©әй–“гҒ«зӣҙдәӨгҒҷгӮӢеә§жЁҷи»ё ![]() и»ёгҖҒ
и»ёгҖҒ![]() и»ё,
и»ё, ![]() и»ёгӮ’еҸ–гҒЈгҒҰеә§жЁҷгӮ’е…ҘгӮҢгӮӢ
и»ёгӮ’еҸ–гҒЈгҒҰеә§жЁҷгӮ’е…ҘгӮҢгӮӢ ![]() еә§жЁҷзі»гҒ§
еә§жЁҷзі»гҒ§ ![]() гҒЁгҒ„гҒҶеә§жЁҷгӮ’жҢҒгҒӨзӮ№
гҒЁгҒ„гҒҶеә§жЁҷгӮ’жҢҒгҒӨзӮ№
![]() гҒ®еҺҹзӮ№гҒӢгӮүгҒ®и·қйӣўгӮ’
гҒ®еҺҹзӮ№гҒӢгӮүгҒ®и·қйӣўгӮ’ ![]() ,
,
![]() и»ёгҒ®жӯЈж–№еҗ‘гҒЁгҒӘгҒҷи§’гӮ’
и»ёгҒ®жӯЈж–№еҗ‘гҒЁгҒӘгҒҷи§’гӮ’ ![]() (
(
![]() ),
),
![]() гӮ’
гӮ’ ![]() е№ійқўгҒ«жӯЈе°„еҪұгҒ—гҒҹзӮ№гӮ’
е№ійқўгҒ«жӯЈе°„еҪұгҒ—гҒҹзӮ№гӮ’
![]() гҒЁгҒ—гҒҰгҖҒ
гҒЁгҒ—гҒҰгҖҒ
![]() гҒҢ
гҒҢ ![]() и»ёгҒ®жӯЈж–№еҗ‘гҒЁгҒӘгҒҷи§’гӮ’
еҸҚжҷӮиЁҲеӣһгӮҠгҒ«иЁҲгҒЈгҒҹи§’еәҰгӮ’
и»ёгҒ®жӯЈж–№еҗ‘гҒЁгҒӘгҒҷи§’гӮ’
еҸҚжҷӮиЁҲеӣһгӮҠгҒ«иЁҲгҒЈгҒҹи§’еәҰгӮ’ ![]() (
(
![]() ) гҒЁгҒҷгӮӢгҒЁ
) гҒЁгҒҷгӮӢгҒЁ
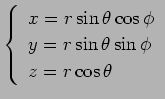
еҶҷеғҸ
йҖҶгҒ®иЁҲз®—гҖҒгҒӨгҒҫгӮҠ ![]() гҒӢгӮү
гҒӢгӮү
![]() гӮ’жұӮгӮҒгӮӢ
гҒ«гҒҜгҖҒ
гӮ’жұӮгӮҒгӮӢ
гҒ«гҒҜгҖҒ![]() ,
, ![]() гҒҜ
гҒҜ
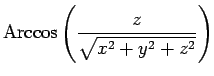 |
гҒӘгҒҠгҖҒ
| з©әй–“жҘөеә§жЁҷгҒ®гғӨгӮігғ“гӮўгғі |
|
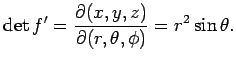
|
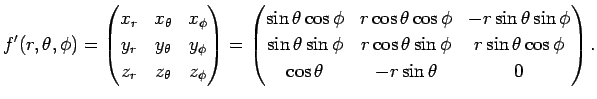
дҫӢгҒҲгҒ°гҖҒгҒҫгҒҡеӨҡйҮҚз·ҡеҪўжҖ§гӮ’дҪҝгҒЈгҒҰгҖҒ
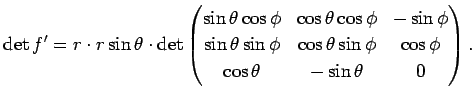
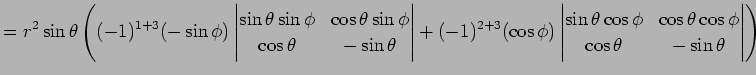 |
||
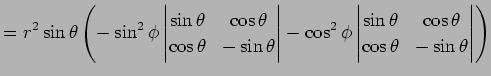 |
||
жЎӮз”° зҘҗеҸІ