- ...微分方程式は解析的1
- 「解析的に解く」とは、不定積分を取る、
四則演算を施す、逆関数を取る、
初等関数に代入するなどで求めたり -- いわゆる求積法で
解いたり -- 、解を級数で表現したりすることを指す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...に解けないことが多い。たとえ解けても便利でないことがある2
- 例え
ば無限級数で解を表したとして、その値を計算するのはそんなに簡単ではない。
無限級数は有限的な表現とは言えない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 法を使い3
- 実は
実際に色々解いてみて、最近考え方が変ってきた。
やはり最低限 RKF45 くらいは使いたい。しっかり解説を書くべきだと思う。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... の連続性を仮定するだけで十分4
- ただしこれは有限次元の場合で、
無限次元の場合は連続性だけではダメである (反例がある)。
連続の場合の存在証明はいわゆるコンパクト性の議論を用いるので、
空間の次元が有限次元であることは本質的な仮定となってしまうのは自然である。
一方、
「
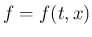 が連続かつ
が連続かつ 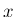 につき局所 Lipschitz 条件を満たすならば、
局所解が一意的に存在する」という定理は無限次元でもそのまま成り立つ。
につき局所 Lipschitz 条件を満たすならば、
局所解が一意的に存在する」という定理は無限次元でもそのまま成り立つ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
一般的に5
- 例えば、
4 段 4 次の公式にはどういうものがありうるかとか、
5 段 5 次の公式は存在しないようだとか。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... の計算回数である6
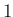 段法なのに「段数」とは?英語では
step, stage と区別があるのだが、日本語では同じ「段」となってしまって紛
らわしい。残念ながら、この用語はもう定着してしまっている。
段法なのに「段数」とは?英語では
step, stage と区別があるのだが、日本語では同じ「段」となってしまって紛
らわしい。残念ながら、この用語はもう定着してしまっている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
呼ぶ7
- 多分
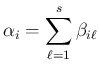 ,
,
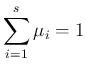 のような条件があるのだと思うが…
のような条件があるのだと思うが…
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
が成り立つことを言う8
- 行列
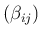 の対角線の上側と対角線上に
ある成分がすべて 0
であること。
つまり
の対角線の上側と対角線上に
ある成分がすべて 0
であること。
つまり
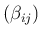 が狭義の下三角行列であるという条件である。
が狭義の下三角行列であるという条件である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
が成り立つ9
-
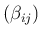 の対角線の上側にある成分が
すべて 0
(対角成分自身は 0
でなくてもよい) ということ。
つまり
の対角線の上側にある成分が
すべて 0
(対角成分自身は 0
でなくてもよい) ということ。
つまり
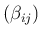 が狭義下三角行列であるという条件である。
が狭義下三角行列であるという条件である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...一松110
- 今ではこの本も古くなったので、
もっと大きな
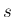 まで分かっているかも知れない。
また別の文献に書いてあることと矛盾していたような覚えがある。
まで分かっているかも知れない。
また別の文献に書いてあることと矛盾していたような覚えがある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... RKF4511
- この公式は
御覧の通り大変複雑である。
筆者はこの公式で誤植のドジを犯したことがある
(レポート課題のプリントで間違えた -- 罪重…)。
この公式を用いたプログラムを書く時は複数の資料でチェックすることをお勧めする。
なお、オリジナルは
E.Fehlberg; ``Klassische Runge-Kutta-Formeln vierter und niedrigerer
Ordnung mit Schrittweiten-Kontrolle und ihre Anwendung auf
Wrmeleitungs-probleme'', Computing, Vol.6, pp.61-71 (1970).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(実行してみると12
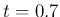 くらいから、
刻み幅の調節が実際に動き始め、
くらいから、
刻み幅の調節が実際に動き始め、
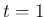 の手前でぐんぐん小さくなっていく。
コンパクトなスペースで紹介するにはどうしたら良いか分からないので
結果はここには載せない
の手前でぐんぐん小さくなっていく。
コンパクトなスペースで紹介するにはどうしたら良いか分からないので
結果はここには載せない
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
13
- 一松先生の本には、
最後の項を $x_0^2$ で割るのを忘れるという、軽い誤植があります。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... に減衰するのに必要な時間のことである14
- 半減期と
いうものに似ている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(日本語で読める本としては珍しいと思われるので貴重15
- この本は非常
に有名だが、叩く人も多くて「悪評」だけ読んでいると敬遠してしまいそう。
しかし参考になるところは多い。
実際この本よりも役立たずの本は世の中にたくさんある。
つまり「この本一冊で OK だ」という捉え方をする人 (欧米では多いらしい) に
警告を発するために批判されているらしい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
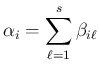 ,
,
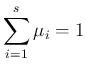 のような条件があるのだと思うが…
のような条件があるのだと思うが…