「実際の計算機で浮動小数点表現が実現される形は、ここで議論する理想的な ものとは異なるかもしれない。しかしその差異は小さく、丸め誤差と いう基本的な問題を扱う場合には常にほとんど無視することが出来る」 -- Forsythe
数値計算で扱う数の範囲は極めて広い。整数や固定小数点数では不便である (ENIAC を開発した von Neumann はそれくらい何でもないと思ったらしいが)。 科学で現れる数の表現には「科学的表記法」 (scientific notaion) (あるいは「指数形式」 (exponential form)) と呼ばれるものがあるが、 これを取り入れたものが、 以下に説明する浮動小数点数 (floating point numbers) である。
以下に見るように、浮動小数点数の体系は数学的にはあまりきれいなもので はなく、実用的な観点からも完璧なものからはほど遠いものである。
この体系とつき合うには、物理や化学の実験でおなじみの有効数字の概念を 勉強した時の感覚が多少は役に立つが、かなり独特のものがあると思う。
基数 ![]() を固定する時、
を固定する時、![]() でない任意の実数
でない任意の実数 ![]() は
は
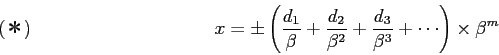
そこで計算機の内部では上式を有限項で打ち切った
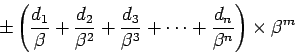
これを ![]() 進
進 ![]() 桁浮動小数点表示と呼び、この形に表現される数を
浮動小数点数 (floating-point numbers) という。
桁浮動小数点表示と呼び、この形に表現される数を
浮動小数点数 (floating-point numbers) という。
現在の実際の計算機で採用されている基数は、主として 2, 10, 16 である (パソコン、ワークステーションでは 2、スーパーコンピューターを除く大型機 では 16 が多い)。
通常は最上位の桁 ![]() は (上に書いたように)
は (上に書いたように) ![]() にならないようにして
おく。この条件を満たしている表示を正規化 (normalize) された浮動小数点表
示という。
にならないようにして
おく。この条件を満たしている表示を正規化 (normalize) された浮動小数点表
示という。
![]() は浮動小数点表示においては特別扱いする。通常はその仮数部を all
zero (
は浮動小数点表示においては特別扱いする。通常はその仮数部を all
zero (
![]() )、指数
)、指数 ![]() とすることにより表現する。
とすることにより表現する。
条件 ![]() ,
,
![]() を満たす全ての (*) に、この
を満たす全ての (*) に、この ![]() を加えたもので一つの浮動小数点の体系
を加えたもので一つの浮動小数点の体系 ![]() が出来る。
が出来る。