数直線上に表してみると、左右に広漠な空きがあること、またゼロの付近も ひどく空いていることに気付く。 これは一般的な特徴である。
実際の計算機では、符号、仮数部、小数部のそれぞれを2進数 (ビットの列)
で表すことになる (![]() が前節で説明した方法で表現される)。
が前節で説明した方法で表現される)。
SPARCstation 上の FORTRAN では、単精度 (32bits) の場合、符号1ビット、 指数部 7 ビット、仮数部 24 ビット (ただしいわゆるケチ表現をしている)。 倍精度の場合は、符号1ビット、指数部 10 bit、仮数部 53 bit である。
問題点
大雑把に言って、浮動小数点数の体系は相対誤差を一定量で押えるよ
うになっている。 ![]() に属する数の絶対値の最大値を
に属する数の絶対値の最大値を ![]() ,
,
![]() に属する数の絶対値の最小値を
に属する数の絶対値の最小値を ![]() とし、
とし、
![]() とおく。
とおく。![]() に対し、
に対し、
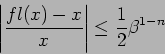
演算の際の丸めについて。 ![]() としても
としても ![]() であるとは
限らない。計算機の中の加算
であるとは
限らない。計算機の中の加算 ![]() はうまく実現した場合で
はうまく実現した場合で
![]() はあまり良い性質を持たない。(
はあまり良い性質を持たない。(![]() が体のような代数系になら
ないのはまあ仕方ないにしても)可換則は OK であるが、結合則や分配則は成
立しない。このことは誤差の解析を難しくする原因になっている。
が体のような代数系になら
ないのはまあ仕方ないにしても)可換則は OK であるが、結合則や分配則は成
立しない。このことは誤差の解析を難しくする原因になっている。
例.
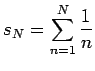 を計算することを
考える。
を計算することを
考える。![]() とした計算例。
とした計算例。
oyabun% test1 s=1.209085083007812e+01 n が小さい方から足していった(単精度) s=1.209015274047852e+01 n が大きい方から足していった(単精度) s=1.209014612986334e+01 n が小さい方から足していった(倍精度) S=1.209014612986341e+01 n が大きい方から足していった(倍精度)
consider
![]()
これは情報落ち(桁揃えの段階で仮数部が捨てられる)と呼ばれる現象。