整数1は数値シミュレーションでは データとして使われることは滅多にないが、 簡単に解説しておく。
![]() ビット・マシンでは、
ビット・マシンでは、![]() ビットのデータ (ワード) を標準の整数デー
タを表現するために使うことが多い。
ビットのデータ (ワード) を標準の整数デー
タを表現するために使うことが多い。![]() ビットで
ビットで ![]() 個のデータを表現
することが出来る (
個のデータを表現
することが出来る (![]() では
では ![]() 個、
個、![]() では
では ![]() 個)。
正の数だけあれば間に合うならば、ごく自然に
個)。
正の数だけあれば間に合うならば、ごく自然に
![]() の数を対
応させることが出来る (実際
の数を対
応させることが出来る (実際
![]() を
を ![]() ビットのデータとして、
ビットのデータとして、
![]() を対応させればよい)。C 言語で ``unsigned (符号無)''
を冠したデータ型はまさにこれである。
を対応させればよい)。C 言語で ``unsigned (符号無)''
を冠したデータ型はまさにこれである。
しかし大抵は負の数をも必要とする。素朴に考えると、1 ビット (例えば
![]() ) を符号を表すのに用いて、残りの
) を符号を表すのに用いて、残りの ![]() ビットで絶対値を表すよう
にする方法が思い浮かぶ。これは絶対値表示と呼ばれ、ある程度使わ
れて来た。しかし現在ポピュラーな方法は補数表示と呼ばれる方法で
ある。大抵は2 の補数表示であるが、1 の補数というものもある。
ビットで絶対値を表すよう
にする方法が思い浮かぶ。これは絶対値表示と呼ばれ、ある程度使わ
れて来た。しかし現在ポピュラーな方法は補数表示と呼ばれる方法で
ある。大抵は2 の補数表示であるが、1 の補数というものもある。
| 1の補数 |
例えば 8 ビットの場合、
|
![]() の補数表示では、
ビット列
の補数表示では、
ビット列
![]() の表す数は
の表す数は
![]() の補数表示を用いる理由は、符号無しの場合の演算をする場合と回路が
共通化出来ること、複数のワードを用いて広い範囲の数を表現する多倍
長整数の演算の実現が簡単なことである。
の補数表示を用いる理由は、符号無しの場合の演算をする場合と回路が
共通化出来ること、複数のワードを用いて広い範囲の数を表現する多倍
長整数の演算の実現が簡単なことである。
演算をすることによって、結果が ![]() ビットの範囲に収まらなくなった場
合は、とにかく下位
ビットの範囲に収まらなくなった場
合は、とにかく下位 ![]() ビットは残し、溢れ出たものは適当に処理する (こ
とが多い)。加算、減算ならば溢れるのは 1 ビットなので、CPU に備わっ
ているフラグに記憶する。乗算の場合は、溢れたものを捨ててしまうか、別の
レジスターに収めることにする。加減算についてはデータを符号無しと考えて
も、符号有りと考えても、結果の下位
ビットは残し、溢れ出たものは適当に処理する (こ
とが多い)。加算、減算ならば溢れるのは 1 ビットなので、CPU に備わっ
ているフラグに記憶する。乗算の場合は、溢れたものを捨ててしまうか、別の
レジスターに収めることにする。加減算についてはデータを符号無しと考えて
も、符号有りと考えても、結果の下位 ![]() ビットは同じものになることに注意。
10進数で説明すると
ビットは同じものになることに注意。
10進数で説明すると
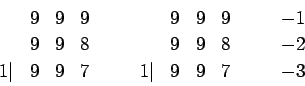
これに対して割算については、正数同士の場合はあまり問題がないが、負数
を含む演算の結果についてはあまり合理的な説明は出来ない。割り切れない場
合、剰余の符号をどう取るか、それに関連して商 (整数) をどうするか。
(![]() ÷
÷ ![]() は ``
は ``![]() 余り
余り ![]() '' なのか、 ``
'' なのか、 ``![]() 余り
余り ![]() '' なのか。
割る数×商+剰余が割られた数にならない場合もある(ひどい)。)
'' なのか。
割る数×商+剰余が割られた数にならない場合もある(ひどい)。)