Next: 3.2.2 Euler(オイラー)法の紹介 Up: 3.2 数値解法(1) Previous: 3.2 数値解法(1)
常微分方程式としては正規形8のもののみを扱います。後で例で見るように、高階の方程式も一階の方程式に
帰着されますから、当面一階の方程式のみを考えます。
独立変数を ![]() 、未知関数を
、未知関数を ![]() とすれば、一階正規形の常微分方程式
とは
とすれば、一階正規形の常微分方程式
とは
| (8) | 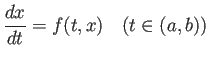 |
| (9) |
常微分方程式の数値解法の基本的な考え方は次のようなものです。「問題と
なっている区間 ![]() を
を
区間 ![]() の分割の仕方ですが、以下では簡単のため
の分割の仕方ですが、以下では簡単のため ![]() 等分すること
にします。つまり
等分すること
にします。つまり