Next: 10 リンク Up: 9 行列の解析的性質で遊ぶ Previous: 9.2 行列の等比級数
簡単のため ![]() 次正方行列
次正方行列 ![]() が対角化可能で、
その固有値を
が対角化可能で、
その固有値を ![]() ,
, ![]() ,
, ![]() ,
それらに属する固有ベクトルを
,
それらに属する固有ベクトルを ![]() ,
, ![]() ,
, ![]() とする。
さらに
とする。
さらに
![]() は他の固有値の絶対値よりも大きいとする。
は他の固有値の絶対値よりも大きいとする。
任意のベクトル ![]() は
は
と展開できるが、
以上のことを Octave による計算で確かめるためには、
![]() がオーバーフローすることを防ぐため、
代りにその長さで割った
がオーバーフローすることを防ぐため、
代りにその長さで割った
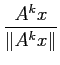 を作ればよい。
を作ればよい。
以下では素朴に ![]() をかけていくことで
をかけていくことで
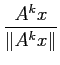 を
求めている。
を
求めている。
octave:5> x=ones(n,1)
octave:5> for i=1:100
> y=a*x
> x=y/norm(y)
> end
octave:5> a*x ./ x
← a*x の各成分を対応する x の成分で割ってみる
octave:5> eig(a)
← 念のため eig() で a の固有値を調べて比較
線形代数では、固有値を固有多項式の根として特徴づけるが、 普通固有多項式を数値計算で解くのは難しいので、 行列の問題のまま各種の反復法を用いることになる。 上で見た方法は『冪乗法』と呼ばれ、多くの方法の基礎となっている。
桂田 祐史
2017-06-19