Next: 2.3 の Euclid ノルム Up: 2. の内積と親しもう Previous: 2.1 この章のねらい
![]() を自然数とするとき、
を自然数とするとき、
![]() ,
,
![]() に対して
に対して
![\begin{jproposition}[内積の公理]
$\R^n$\ における内積について以...
...l x$, $y\in\R^n$\ に対して
$(x,y)=(y,x)$.
\end{enumerate}\end{jproposition}](img4.gif)
|
我々は後で上の (1), (2), (3) を満たす
![]() を
一般に内積と呼ぶことになる。
つまり内積の概念を一般化するので、
(2.1) で定義される
を
一般に内積と呼ぶことになる。
つまり内積の概念を一般化するので、
(2.1) で定義される ![]() のことを
のことを
![]() の標準内積または Euclid 内積と呼ぶことにする。
の標準内積または Euclid 内積と呼ぶことにする。
が成り立つことに注意しておくと便利である。 例えば行列の積に関する結合則と、 公式
が分かる。 ゆえに
![\begin{jproposition}[対称性の内積による特徴付け]
$A\in \R^{n\times...
...all x,y\in\R^n$\ に対して $(Ax,y)=(x,Ay)$.
\end{enumerate}\end{jproposition}](img5.gif)
|
これが任意の
有名な Schwarz の不等式は、何と言っても基本的である。
![\begin{jproposition}[Schwarz の不等式]
任意の $x$, $y\in\R^n$\ に対し...
...x$\ と $y$\ が $1$\ 次従属のときのみ成立する。
\end{jproposition}](img6.gif)
|
左辺を展開して
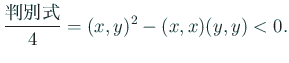
ゆえに
一方、
桂田 祐史