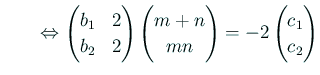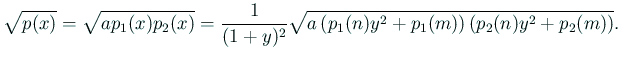- (i)
 が相異なる3実根 を持つ場合。
が相異なる3実根 を持つ場合。
と書ける。
- (a)
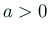 の場合、
の場合、
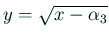 とおくと、
とおくと、
 .
.
- (b)
 の場合、
の場合、
 とおくと、
とおくと、
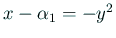 .
.
- (ii)
 が唯1つの実根
が唯1つの実根 を持つ場合、
を持つ場合、
と書ける。
とおくと、
 であるから、
であるから、
 は
は
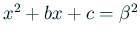 の根であるので、
の根であるので、
ゆえに
- (iii)
 が少なくとも1つの虚根
が少なくとも1つの虚根 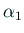 を持つ4次式の場合は、
共役複素数
を持つ4次式の場合は、
共役複素数
 も根である。
他の2根を
も根である。
他の2根を 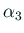 ,
,  と表し、
と表し、
とおくと、 と
と 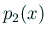 はともに実係数
はともに実係数 次多項式で、
次多項式で、
 は既約であり、
は既約であり、
と書ける。
- (a)
 ならば、
ならば、
とおくと、
- (b)
-
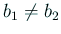 の場合。
まず、2次方程式
の場合。
まず、2次方程式
( ) ) |
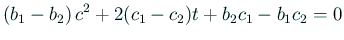 |
は相異なる2実根を持つことを示す。実際、
であるから、判別式 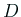 は、
は、
一方
であるから、
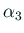 ,
,  が実数であるときは、
が実数であるときは、
 が既約であることから、
が既約であることから、
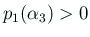 ,
,
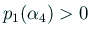 であるから、
であるから、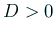 .
一方、
.
一方、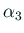 ,
,  が虚数であるときは、互いに複素共役であるから、
が虚数であるときは、互いに複素共役であるから、
 が実係数であることから、
が実係数であることから、
 .
ゆえに
.
ゆえに
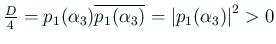 .
いずれの場合も、(
.
いずれの場合も、( ) の判別式が正であるから、
(
) の判別式が正であるから、
( ) は相異なる2実根
) は相異なる2実根 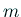 ,
,  を持つ。
を持つ。
とおくと、
であり、
ところが  ,
, 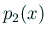 の右辺の (
の右辺の ( について) 1 次の係数はともに
0
である。実際、
について) 1 次の係数はともに
0
である。実際、
ゆえに
- (iv)
- (工事中)
桂田 祐史
![$\displaystyle \beta=
\left\{
\begin{array}[tb]{ll}
\sqrt{p_1(\alpha)} & \tex...
...lpha< 0$)},
\end{array} \right.
\quad
m=\alpha+\beta,\quad
n=\alpha-\beta,
$](img532.gif)
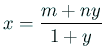


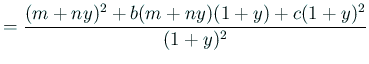
![$\displaystyle =\frac{1}{(1+y)^2} \left[ m^2+2mny+n^2y^2+b(ny^2+(n+m)y+m)+c(y^2+2y+1) \right]$](img538.gif)
![$\displaystyle =\frac{1}{(1+y)^2} \left[ (n^2+bn+c)y^2+(2mn+b(n+m)+2c)y+m^2+bm+c \right]$](img539.gif)
![$\displaystyle =\frac{1}{(1+y)^2} \left[ p_1(n)y^2+\left[2(\alpha^2-\beta^2)+b\cdot 2\alpha+2c\right]+p_1(m) \right]$](img540.gif)
![$\displaystyle =\frac{1}{(1+y)^2} \left[ p_1(n)y^2+2(\alpha^2+b\alpha+c-\beta^2)+p_1(m) \right].$](img541.gif)
![$\displaystyle p_1(x)=\frac{1}{(1+y)^2}\left[p_1(n)y^2+p_1(m)\right].
$](img544.gif)
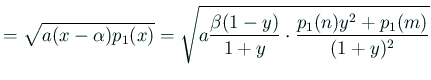


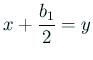
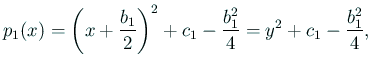


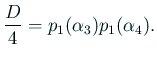
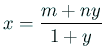


![$\displaystyle =\frac{1}{(1+y)^2} \left[p_1(n)y^2+\left(2mn+b_1(n+m)+2c_1\right)y+p_1(m)\right],$](img585.gif)
![$\displaystyle =\frac{1}{(1+y)^2} \left[p_2(n)y^2+\left(2mn+b_2(n+m)+2c_2\right)y+p_2(m)\right].$](img587.gif)