- まだ全体像が見えていないけれど、
楕円積分、楕円関数は、どうやらとても上手く標準化出来ているらしい。
- AGM は楕円積分、楕円関数の計算に幅広く利用でき、また非常に効率的である。
倍精度の値を得るために、反復回数は 5 回程度
(AGM は2次の収束をするので、そんなものなのだろう)。
楕円関数を計算するためには、
反復1回ごとに平方根、
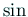 ,
, 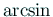 が必要になるが、
5回ならばそれほど大変ではない。
が必要になるが、
5回ならばそれほど大変ではない。
- 複素関数としての Jacobi の楕円関数の計算に必要な算術幾何平均の計算は、
実関数の場合のちょうど2倍程度。これ本当かな?
なんとうまく出来ているのだろう。
- 楕円積分は、導関数が初等関数では求められなくても、
非常に効率的な計算法が確立されていた、ということのようだ。
Gauss が
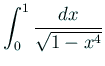 を高精度に計算していたのは、
きわめて自然だったわけだ。
を高精度に計算していたのは、
きわめて自然だったわけだ。
なんか、すごく面白いんですけど。
桂田 祐史
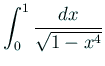 を高精度に計算していたのは、
きわめて自然だったわけだ。
を高精度に計算していたのは、
きわめて自然だったわけだ。