Next: 5.3 Weierstrassの楕円関数 Up: 5 一般の楕円関数と Weierstrassの楕円関数 Previous: 5.1 二重周期有理型関数としての楕円関数
|
|
|
|
|
|
![]() の周期性から、
の周期性から、![]() に属する極における留数の和と、
に属する極における留数の和と、
![]() に属する極における留数の和は等しいので、
に属する極における留数の和は等しいので、
![]() について留数の和が 0 であることを示せば良い。
ゆえに最初から
について留数の和が 0 であることを示せば良い。
ゆえに最初から ![]() の周上に極がないとして示せば良い。
の周上に極がないとして示せば良い。
![]() の周に沿って正の向きに一周する閉曲線
の周に沿って正の向きに一周する閉曲線 ![]() に沿う線積分は、
周期性から0に等しい。
留数定理によって、その
に沿う線積分は、
周期性から0に等しい。
留数定理によって、その ![]() 内部の留数の和は0に等しい。
内部の留数の和は0に等しい。 ![]()
![]()
|
(基本領域の選び方によらずに定まることに注意せよ。) |
|
|
|
|
![]() を楕円関数とする。
を楕円関数とする。![]() の周期は
の周期は ![]() の周期でもあり
の周期でもあり
![]() の周期でもある。
の周期でもある。
![]() の周を正の向きに一周する閉曲線
の周を正の向きに一周する閉曲線 ![]() について、
偏角の原理から
について、
偏角の原理から
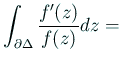 零点の位数の和
零点の位数の和
![\begin{jproposition}[Abelの定理 (Liouvilleの第4定理)]
位数が2以上�...
...aymath} ただし $\Gamma$ は $f$ の周期群である。
\end{jproposition}](img370.gif)
|