Next: 4 AGM Up: 3 Jacobiの楕円関数 Previous: 3.4 全体への拡張
![]() とする。
複素平面内の長方形の4頂点となる
0,
とする。
複素平面内の長方形の4頂点となる
0, ![]() ,
,
![]() ,
, ![]() を
を
![]() ,
,
![]() ,
,
![]() ,
,
![]() と名付ける。
と名付ける。
![\includegraphics[width=10cm]{graph/scdn.eps}](img245.gif)
 ,
0 が極ならば
,
0 が極ならば
 ,
0 が零点でも極でもなければ
,
0 が零点でも極でもなければ
 .
.
![]() について、0 が零点であり、
について、0 が零点であり、![]() が極である。
が極である。
![]() は周期である。一方
は周期である。一方 ![]() は周期であるが、
は周期であるが、![]() は周期ではない。
は周期ではない。
12個の楕円関数のいずれも、
![]() ,
, ![]() ,
,
![]() を周期とする。
それぞれの楕円関数は、
(上に書いた周期の半分)
を周期とする。
それぞれの楕円関数は、
(上に書いた周期の半分) ![]() ,
, ![]() ,
,
![]() のうち、
いずれか一つだけを周期に持つ。
のうち、
いずれか一つだけを周期に持つ。
|
|
|
|
|
||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
これらの関数は次の関係式を満たす。
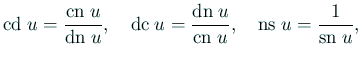 | ||
 | ||
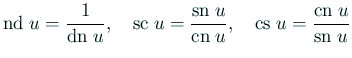 |
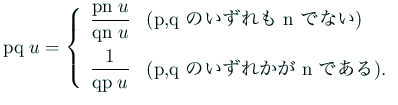
我々は、
![]() を極とする楕円関数
を極とする楕円関数 ![]() ,
, ![]() ,
, ![]() を選んだ。
この
を選んだ。
この![]() つがあれば、他の9個の楕円関数を表すことが出来る。
めでたし、めでたし、と考えられる。
つがあれば、他の9個の楕円関数を表すことが出来る。
めでたし、めでたし、と考えられる。
三角関数は6種類あるが、![]() ,
, ![]() の2つを使えば、
他の4個の三角関数を表すことが出来る3、というのに似ている。
の2つを使えば、
他の4個の三角関数を表すことが出来る3、というのに似ている。
![]() ,
, ![]() ,
, ![]() はいずれも、
はいずれも、
![]() が半周期で、
が半周期で、![]() が
が
![]() 周期である。
つまり
周期である。
つまり
![]() の零点は
の零点は
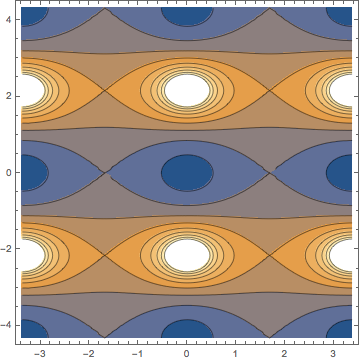
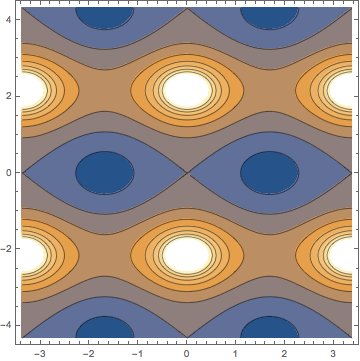
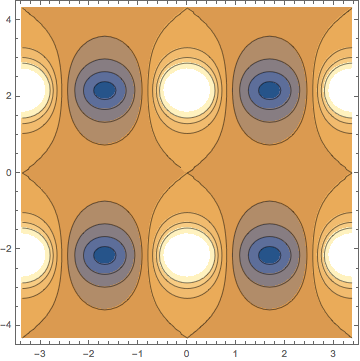
| Jacobiの楕円関数の零点と極の位置の確認 |
k=0.5; m=k^2; m1=1-m; K=EllipticK[m]; Kp=EllipticK[m1];
gAbsSn=ContourPlot[Abs[JacobiSN[x+I*y,m]], {x,-2K,2K}, {y,-2Kp,2Kp}]
gAbsCn=ContourPlot[Abs[JacobiCN[x+I*y,m]], {x,-2K,2K}, {y,-2Kp,2Kp}]
gAbsDn=ContourPlot[Abs[JacobiDN[x+I*y,m]], {x,-2K,2K}, {y,-2Kp,2Kp}]
Export["AbsSn.pdf",gAbsSn]
Export["AbsSn.png",gAbsSn]
Export["AbsCn.pdf",gAbsCn]
Export["AbsCn.png",gAbsCn]
Export["AbsDn.pdf",gAbsDn]
Export["AbsDn.png",gAbsDn]
|
|
|
|
零点の位置、極の位置が、ぱっと頭に浮かぶようになるだろうか?
![]() ,
, ![]() ,
, ![]() は、
は、
![]() が
が
![]() 周期、
周期、![]() が半周期である
(
が半周期である
(![]() については
については ![]() が周期、
が周期、![]() については
については ![]() が周期という方が分かる?)。
どの関数も、零点と極はともに
が周期という方が分かる?)。
どの関数も、零点と極はともに ![]() ,
, ![]() を周期として現れる。
どの関数も、基本領域内の零点の数と極の数はともに
を周期として現れる。
どの関数も、基本領域内の零点の数と極の数はともに ![]() である
(零点の個数と極の個数が等しいのは楕円関数の基本的な性質である)。
である
(零点の個数と極の個数が等しいのは楕円関数の基本的な性質である)。
![]() を頂点とする長方形内(基本領域2つ分)には
を頂点とする長方形内(基本領域2つ分)には ![]() 個ずつある。
個ずつある。
![]() ,
, ![]() の実関数のグラフを知っていると零点の位置は分かる
(
の実関数のグラフを知っていると零点の位置は分かる
(![]() ,
, ![]() )。
)。![]() は
は
![]() で 0:
で 0:
![]() 名前の2文字目がともに
名前の2文字目がともに
![]() なので、
なので、![]() に極があることが分かる。
に極があることが分かる。
桂田 祐史