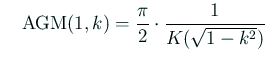2.5 Legendreの関係式

(準備中)

四ッ谷・村井 [13] にあるが、桂田 [5] の付録 E「楕円積分とAGM」もチェックすること。ここを完備化するよりも [5] を完成させる方が良い。

$\begin{jproposition}[Legendreの関係式] $0\le k<1$ \begin{equation} \frac{E(... ...}\cdot\frac{1}{K(k)K\left(\sqrt{1-k^2}\right)}. \end{equation}\end{jproposition}$

次の2つの命題によって、, が AGM で計算できることが分かる。有限項で切った時の評価式が村井・松本・四ッ谷 [17] で発表されている ([13])。

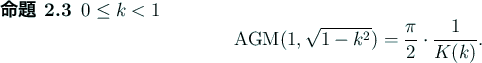
$\begin{jproposition} $0\le k<1$ \begin{displaymath} \mathrm{AGM}(1,\sqrt{1-k^2})=\frac{\pi}{2}\cdot\frac{1}{K(k)}. \end{displaymath}\end{jproposition}$

$\begin{jproposition} $0\le k<1$ \begin{displaymath} \frac{E(k)}{K(k)}=1-\sum_{n=0}^\infty 2^{n-1}c_n^2. \end{displaymath}\end{jproposition}$

$\begin{jproposition}[Gauss] \begin{displaymath} \pi=\frac{2\mathrm{AGM}(1,1/\sq... ...t(1-m^2\right)} \quad\text{(変な感じ)}. \end{displaymath}\end{jproposition}$

えーと、以前書いたノートにも

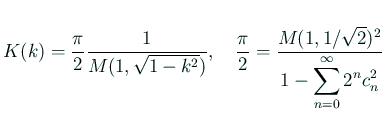
$\displaystyle K(k)=\frac{\pi}{2}\frac{1}{M(1,\sqrt{1-k^2})},\quad \frac{\pi}{2}=\frac{M(1,1/\sqrt{2})^2}{1-\dsp\sum_{n=0}^\infty 2^n c_n^2}$

とある。 $\pi$ を表す公式は一致している。

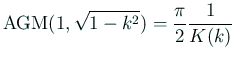$\displaystyle \mathrm{AGM}(1,\sqrt{1-k^2})=\frac{\pi}{2}\frac{1}{K(k)}$ だから $\displaystyle \quad \mathrm{AGM}(1,k)=\frac{\pi}{2}\cdot\frac{1}{K(\sqrt{1-k^2})}$

桂田祐史