Next: 2.2.3 Weierstrassの標準形 Up: 2.2 標準形 Previous: 2.2.1 Legendre-Jacobi の標準形
![]() のときの
のときの ![]() の値 (あるいは
の値 (あるいは
![]() のときの
のときの
![]() の値) は、
楕円関数の周期と関係するので特に重要で、特別に記号が用意されている。
の値) は、
楕円関数の周期と関係するので特に重要で、特別に記号が用意されている。
| (6) |  |
| (7) |
| (8) |
| 記憶用 |
|

|
| 例えば |
|
|
| 記憶用の式 |
|
母数
|
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
 のどれか一つが
与えられれば、他は定まる。
のどれか一つが
与えられれば、他は定まる。
(実際、容易に分かるように、
![]() は狭義単調増加である。
は狭義単調増加である。

| (9) | 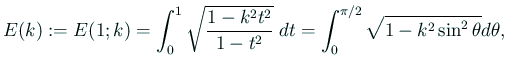 | |
| (10) |  |
| Mathematica でグラフを描く | |||||||||
Mathematica では
を計算する関数 EllipticK[m], EllipticE[m], EllipticPi[n,m] が用意されている。母数
grK = Plot[EllipticK[k^2], {k, 0, 0.99999}, PlotRange -> {0, 8}]
grE = Plot[EllipticE[k^2], {k, 0, 1}, PlotRange -> {0, 2}]
grPi = Plot[EllipticPi[-3/4, k^2], {k, 0, 1}, PlotRange -> {0, 3}]
とすることになる。
|
![\includegraphics[width=0.9\textwidth]{graph/graph-K.eps}](img142.gif)
|
![\includegraphics[width=0.9\textwidth]{graph/graph-E.eps}](img143.gif)
|
![\includegraphics[width=0.9\textwidth]{graph/graph-Pi.eps}](img144.gif)
|
桂田 祐史