Next: 2.2.2 т«їтЁеТЦЋтєєуЕЇтѕє Up: 2.2 ТеЎТ║ќтйб Previous: 2.2 ТеЎТ║ќтйб
ТЦЋтєєуЕЇтѕєсЂ»тцЅТЋ░тцЅТЈЏсЂет╝ЈтцЅтйбсЂФсѓѕсѓісђЂТгАсЂ«3уе«жАъсЂ«уЕЇтѕєсЂетѕЮуГЅжќбТЋ░сЂДУАесЂЋсѓїсѓІ
(сЂЮсЂєсЂа)сђѓ
![]() сЂесЂЌсЂдсђЂ
сЂесЂЌсЂдсђЂ
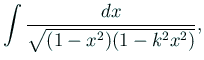 | ||
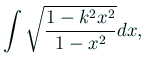 | ||
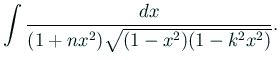 |
| (2) |  | |
| (3) | 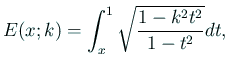 | |
| (4) | 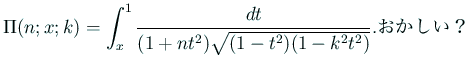 |
![]() сѓњТ»ЇТЋ░ ((elliptic) modulus,
eccentricity),
сѓњТ»ЇТЋ░ ((elliptic) modulus,
eccentricity), ![]() сѓњсЃЉсЃЕсЃАсЃ╝сѓ┐сЃ╝сЂетЉ╝сЂХсђѓ
сѓњсЃЉсЃЕсЃАсЃ╝сѓ┐сЃ╝сЂетЉ╝сЂХсђѓ
![]() сЂ» (жђџтИИ)
сЂ» (жђџтИИ)
![]() сЂ«у»ётЏ▓сѓњтІЋсЂЈсђѓ
сЂ«у»ётЏ▓сѓњтІЋсЂЈсђѓ
![]() сЂ«С╗БсѓЈсѓісЂФсђЂ
сЂ«С╗БсѓЈсѓісЂФсђЂ
![]() ,
,
![]() сЂесЂфсѓІ
сЂесЂфсѓІ ![]() сѓњСй┐сЂєсЂЊсЂесѓѓтцџсЂёсђѓ
сѓњСй┐сЂєсЂЊсЂесѓѓтцџсЂёсђѓ
![]() сѓњ modular angle сЂетЉ╝сЂХсђѓ
сѓњ modular angle сЂетЉ╝сЂХсђѓ
![]() сЂ«С╗БсѓЈсѓісЂФсђЂ
сЂ«С╗БсѓЈсѓісЂФсђЂ![]() сЂесЂфсѓІ
сЂесЂфсѓІ ![]() сѓњСй┐сЂєТхЂтёђсѓѓсЂѓсѓІ (тЅ▓сЂетцџсЂё)сђѓ
сѓњСй┐сЂєТхЂтёђсѓѓсЂѓсѓІ (тЅ▓сЂетцџсЂё)сђѓ
![]() сѓњсЃЉсЃЕсЃАсЃ╝сѓ┐сЃ╝сЂетЉ╝сЂХсђѓ
сѓњсЃЉсЃЕсЃАсЃ╝сѓ┐сЃ╝сЂетЉ╝сЂХсђѓ
| УдџсЂѕсЂдсЂісЂЈсЂ╣сЂЇт╝Ј |
|
|
СИђТќ╣сЂДсђЂ![]() сЂ«С╗БсѓЈсѓісЂФсђЂ
сЂ«С╗БсѓЈсѓісЂФсђЂ
![]() сѓњТ║ђсЂЪсЂЎ
сѓњТ║ђсЂЪсЂЎ ![]() сѓњтцЅТЋ░сЂФТјАућесЂЎсѓІсЂЊсЂесѓѓсЂѓсѓІсђѓ
сѓњтцЅТЋ░сЂФТјАућесЂЎсѓІсЂЊсЂесѓѓсЂѓсѓІсђѓ
![]() сѓњ amplitudeсЂетЉ╝сЂХсђѓ
сѓњ amplitudeсЂетЉ╝сЂХсђѓ
(
![]() сЂетцЅТЋ░тцЅТЈЏсЂЌсЂд)
сЂетцЅТЋ░тцЅТЈЏсЂЌсЂд)
 | ||
 | ||
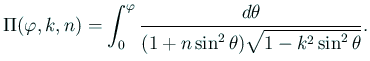 |
![]() сЂ«та┤тљѕсЂ»сђЂ
сЂ«та┤тљѕсЂ»сђЂ![]() сЂ»тѕЮуГЅжќбТЋ░сЂДУАесЂЎсЂЊсЂесЂїсЂДсЂЇсѓІсђѓ
сЂ»тѕЮуГЅжќбТЋ░сЂДУАесЂЎсЂЊсЂесЂїсЂДсЂЇсѓІсђѓ
![]() сЂ«сЂесЂЇсђЂ
сЂ«сЂесЂЇсђЂ
![]() сЂФт»ЙсЂЌсЂдсђЂ
сЂФт»ЙсЂЌсЂдсђЂ
![]() (
(
![]() ) сЂесЂфсѓІ
) сЂесЂфсѓІ ![]() сѓњтЈќсѓІсЂесђЂ
сѓњтЈќсѓІсЂесђЂ
![]() сЂесЂёсЂєтцЅТЋ░тцЅТЈЏсЂД
сЂесЂёсЂєтцЅТЋ░тцЅТЈЏсЂД
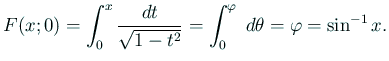
![]() сЂ«сЂесЂЇсђЂ
сЂ«сЂесЂЇсђЂ
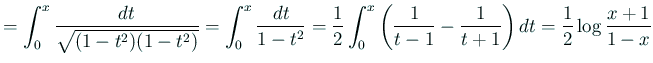 | ||
сЂЙсЂесѓЂсЂдсЂісЂЈсђѓ
| (5) | 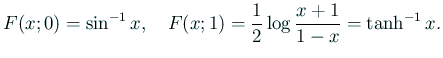 |
![\begin{jremark}[УеўтЈисЂ«ТхЂтёђсЂФсЂцсЂёсЂд]
сЂЕсѓЊсЂфТюгсѓњУфГсѓђТЎѓсѓѓсђЂсЂЮс...
...»сђЂтЇ┤сЂБсЂдТиитљїсЂЌсЂФсЂЈсЂЈсЂдУЅ»сЂёсЂІсѓѓсЂЌсѓїсЂфсЂёсђѓ \qed
\end{jremark}](img106.gif)
ТАѓућ░ уЦљтЈ▓