これが「数式処理」という言葉にもっともしっくり来る計算でしょうか
(英語を覚えていないと大変かも知れませんが…頑張って下さい)。
| 文字式の計算 (1) |
| Expand[(1+x)^10] |
多項式の展開 |
| Factor[x^3+y^3+z^3
- 3 x y z] |
多項式の因数分解 |
| Apart[1/(x^3-1)] |
部分分数への分解 |
| 2 f[x] + 3 f[x] |
|
| |
|
| p1 = Expand[(1+x)^10] |
多項式の展開結果を変数に代入 |
| p2 = (1+x)^3 |
|
| PolynomialQuotient[p1,p2,x] |
多項式の商 |
| PolynomialRemainder[p1,p2,x] |
多項式の剰余 |
| PolynomialQuotientRemainder[p1,p2,x] |
多項式の商と剰余 (同時に求める) |
| Remove[p1,p2] |
おそうじ |
|
有理数・有理式に対して、Numerator[], Denominator[] で
分子、分母を取り出すことが出来る。
多項式 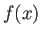 と
と 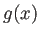 の最大公約多項式を
の最大公約多項式を 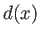 とするとき、
とするとき、
を満たす多項式 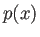 ,
, 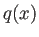 が存在する
(Euclid の互除法によって、
が存在する
(Euclid の互除法によって、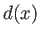 と同時に計算できる)
が、
PolynomialExtendedGCD[] は
と同時に計算できる)
が、
PolynomialExtendedGCD[] は 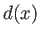 ,
, 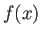 ,
,
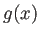 を求めることが出来る。
を求めることが出来る。
| 文字式の計算 (2) |
| f=x^6+1 |
|
| g=x^3-2x^2+x-2 |
|
| PolynomialGCD[f,g] |
最大公約多項式 |
| PolynomialExtendedGCD[f,g,x] |
最大公約多項式 |
| |
|
| Discriminant[a x^2+b x+c,x] |
おなじみ
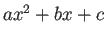 の判別式 の判別式 |
| Discriminant[x^3+p x+q,x] |
3次式の判別式は見たことがないかな? |
| Remove[f,g] |
おそうじ |
|
(余談: 最近 (2011年のこと)、
16次多項式の判別式の計算に成功したというニュースがありました。
38億近い項数だそうです。次数が高くなると、急激に大変になるんですね。)
終結式を計算する Resultant[],
グレブナー基底を計算する GroebnerBasis[] なども用意されています
(高校数学には出て来ない、ちょっと高級な概念)。
桂田 祐史
![]() と
と ![]() の最大公約多項式を
の最大公約多項式を ![]() とするとき、
とするとき、