

Next: D..6.1 Mathematicaでやってみる
Up: D. Mathematicaの多変数の微積分への応用
Previous: D..5.1 Mathematicaでやってみる
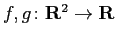 を
を
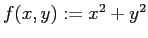 ,
,
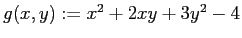 で定め、
で定め、
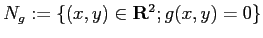 とおく。
とおく。
(1) 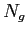 は
は 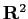 の有界閉集合であることを示せ。
(2) 条件
の有界閉集合であることを示せ。
(2) 条件 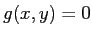 のもとでの
のもとでの 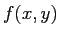 の最大値と最小値を求めよ。
の最大値と最小値を求めよ。
Subsections


Next: D..6.1 Mathematicaでやってみる
Up: D. Mathematicaの多変数の微積分への応用
Previous: D..5.1 Mathematicaでやってみる
桂田 祐史
2013-04-09