

Next: D..5.1 Mathematicaでやってみる
Up: D. Mathematicaの多変数の微積分への応用
Previous: D..4.1 Mathematicaでやってみよう
どちらか一方を選んで解答せよ。
(1)
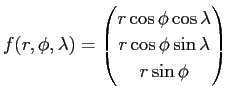 に対して、
に対して、
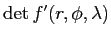 を求めよ。
(2)
を求めよ。
(2)
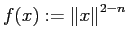 (
(
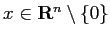 ) とおくとき、
) とおくとき、
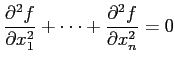 を示せ。
を示せ。
Subsections


Next: D..5.1 Mathematicaでやってみる
Up: D. Mathematicaの多変数の微積分への応用
Previous: D..4.1 Mathematicaでやってみよう
桂田 祐史
2013-04-09
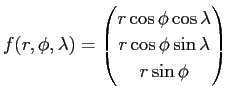 に対して、
に対して、
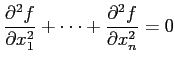 を示せ。
を示せ。