| Integrate[1/(1+x^2),x] |
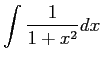
|
| Integrate[x^2,{x,0,1}] |
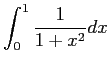
|
| Integrate[E^(-x^2),{x,0,Infinity}] |
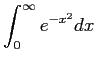
|
不定積分は Integrate[式, 変数], 定積分は Integrate[式, 変数の範囲] とします。
|
定積分の場合、数値積分版 NIntegrate[] もあります。 近似値しか計算できませんが、 Integrate[] では計算できないような定積分も扱えます。
|
文字定数を含んだ関数の積分をするとき、 その定数が正数であるとか、実数であるとか、 Mathematica に教えてやらないと計算出来ないこともあります。
Assuming[a>0, Integrate[Exp[-x^2]Cos[2a x],{x,-Infinity,Infinity}]
Integrate[Exp[-x^2]Cos[2a x],{x,-Infinity,Infinity}, Assumptions->{a>0}]
Integrate[Exp[-x^2]Cos[2a x],{x,-Infinity,Infinity}, Assumptions->Im[a]==0]
|
限定的ですが、
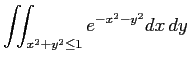 のような重積分も出来ます
(重積分の計算については、誰かレポートを書いてくれないかな…)。
のような重積分も出来ます
(重積分の計算については、誰かレポートを書いてくれないかな…)。
Integrate[Exp[-x^2-y^2] Boole[x^2+y^2<=1], {x,-1,1}, {y,-1,1}]
|