In[1] := Table[Cos[2Pi/n],{n,20}]
あるいは
In[2] := Table[{n,Cos[2Pi/n]},{n,20}]
|
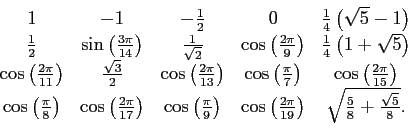
知っている値が多いでしょう。簡単になっていませんが、 実は
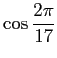 は
は
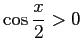 であれば、
であれば、
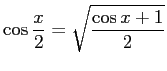
であるから、
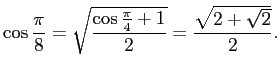
これを確かめるには、引き算して FullSimplify[ ] すると良い:
In[3] := FullSimplify[Cos[Pi/8]-Sqrt[2+Sqrt[2]]/2] |
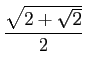 は得られないことである。
一方、
は得られないことである。
一方、
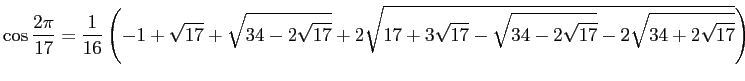
です1。
In[4] := a = (-1 + Sqrt[17] + Sqrt[34 - 2 Sqrt[17]] +
2 Sqrt[17 + 3 Sqrt[17] - Sqrt[34 - 2 Sqrt[17]] -
2 Sqrt[34 + 2 Sqrt[17]]])/16 - Cos[2 Pi/17]
In[5] := FullSimplify[a]
|
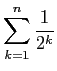 という形なので、
それを計算する関数を定義するのが第一歩。
という形なので、
それを計算する関数を定義するのが第一歩。
In[6] := mysum[n_]:=Sum[1/2^k,{k,1,n}]
|
In[7] := a=mysum[{3,5,10,50}]
|
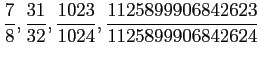
小数点以下
In[8] := N[a,60+1] |
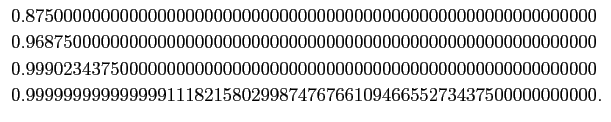
In[8]:= mysum10n[n_] := 10^n Sum[1/2^k, {k, 1, n}]
In[9]:= mysum10n[{3,5,10,50}]
|
つまり
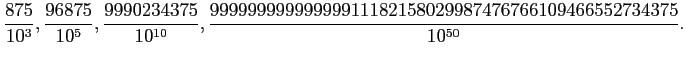
In[] := a=3
In[] := x[1]=1
In[] := x[n_]:=x[n]=(x[n-1]+a/x[n-1])/2
In[] := tablex=Table[x[n],{n,1,10}]
In[] := N[tablex,50+1]
|

第8項目までで、小数点以下
In[] := N[Abs[N[tablex,100]-Sqrt[3]]] |
となります。大雑把に言って、 合致する桁数 (1, 2, 4, 9, 18, 37, 73 と) が倍々ゲームで増えていくことが分かります。 誤差の常用対数をプロットして見ると
![\includegraphics[width=10cm]{eps/errornewton.eps}](img32.png)
- (a)
- 楕円面
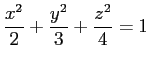 を歪めずに
描くには BoxRatios->Automatic とするのが簡単でしょう。
を歪めずに
描くには BoxRatios->Automatic とするのが簡単でしょう。
一度に描いてしまうことも出来ます。 みんな等値面 (レベルセット) として描いてしまう:
あるいは、みんな関数のグラフとして描いてしまう:In[] := ContourPlot3D[{x^2/2 + y^2/3 + z^2/4 == 1, x + y + z == 3, x + y + z == -3}, {x, -2, 2}, {y, -2, 2}, {z, -7, 7}, BoxRatios -> Automatic]
しかし、別々に描いて合成する方法をマスターすることを勧めたいです (考え方として自然だと思います)。 別々に描いてよいならば、曲面ごとに描く方法を選択できて、 自由度が大きくなるので。In[] := Plot3D[{Sqrt[4 (1 - x^2/2 - y^2/3)], -Sqrt[4 (1 - x^2/2 - y^2/3)], -x - y - 3, -x - y + 3}, {x, -2, 2}, {y, -2, 2}, BoxRatios -> Automatic]平面はグラフとして、楕円面は等値面として描く:
この場合、Show[ ] の引数の順番は大事です。 大きいものを最初に持ってきます。In[] := L=2; In[] := g1=Plot3D[{-x-y-3,-x-y+3},{x,-L,L},{y,-L,L},BoxRatios->Automatic] In[] := g2=ContourPlot3D[x^2/2+y^2/3+z^2/4==1,{x,-L,L},{y,-L,L},{z,-L,L}] In[] := g=Show[g1,g2]しかし、PlotRange->All というオプションに気がつけば、 細かいことを気にする必要はありません。 一つ一つ描いて、最後に順番を気にしないでまとめます:
In[] := g1=Plot3D[-x-y-3,{x,-L,L},{y,-L,L}] In[] := g2=Plot3D[-x-y+3,{x,-L,L},{y,-L,L}] In[] := g3=ContourPlot3D[x^2/2+y^2/3+z^2/4==1,{x,-L,L},{y,-L,L},{z,-L,L}] In[] := Show[g1,g2,g3,PlotRange->All, BoxRatios->Automatic] - (b)
- 軸が
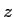 軸で、頂点が原点である直円錐を描くことにします。
軸で、頂点が原点である直円錐を描くことにします。
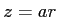 (
(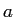 は定数) から、グラフとしての表現
は定数) から、グラフとしての表現
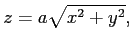
パラメーター曲面としての表現、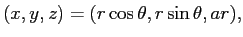
方程式の解集合 (≒関数のレベルセット) としての表現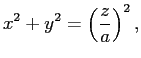 あるいは
あるいは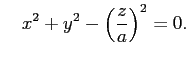
前のページに描いたように、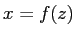 を
を 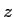 軸のまわりに回転してできる曲面という考え方をすると、
方程式は
軸のまわりに回転してできる曲面という考え方をすると、
方程式は
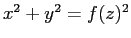 となります。
となります。
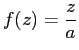 とすると、
上の方程式が得られます。
とすると、
上の方程式が得られます。
g = Plot3D[3 Sqrt[x^2 + y^2] Boole[x^2 + y^2 <= 1], {x, -1, 1}, {y, -1, 1}, BoxRatios -> Automatic]g = ParametricPlot3D[{r Cos[t], r Sin[t], 3 r}, {r, 0, 1}, {t, 0, 2 Pi}]g = ContourPlot3D[x^2 + y^2 - (z/3)^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -3, 3}, BoxRatios -> Automatic]