

Next: B..5.4 QR 分解
Up: B..5 行列の分解について
Previous: B..5.2 三角行列係数の連立1次方程式
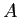 が正値対称行列である場合、
が正値対称行列である場合、
を満たす下三角行列 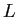 が存在する。これを Cholesky 分解と呼ぶ。
が存在する。これを Cholesky 分解と呼ぶ。
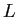 の対角成分は正であるように取ることができるが、
そういうものに限ると分解は一意的である。
の対角成分は正であるように取ることができるが、
そういうものに限ると分解は一意的である。
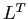 は上三角行列であるから、Cholesky 分解は一種の LU 分解である。
は上三角行列であるから、Cholesky 分解は一種の LU 分解である。
Cholesky 分解は、通常の LU 分解の半分程度の計算量で計算できる (具体的
な計算法は省略)。


Next: B..5.4 QR 分解
Up: B..5 行列の分解について
Previous: B..5.2 三角行列係数の連立1次方程式
桂田 祐史
2012-07-11
![]() が正値対称行列である場合、
が正値対称行列である場合、
![]() は上三角行列であるから、Cholesky 分解は一種の LU 分解である。
は上三角行列であるから、Cholesky 分解は一種の LU 分解である。