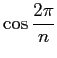 (
(
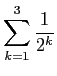 ,
,
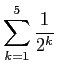 ,
,
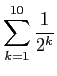 ,
,
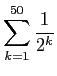 を計算せよ (なるべくユーザー定義関数を使うこと)。
また、それらの値を正確に小数に直せ
(十進法では有限小数というのはすぐ分かりますね?)。
を計算せよ (なるべくユーザー定義関数を使うこと)。
また、それらの値を正確に小数に直せ
(十進法では有限小数というのはすぐ分かりますね?)。
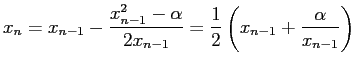 |
が利用できる1。 実際にこれを用いて
- (a)
- 図1を再現せよ。(色々な描き方があります。 楕円面と平面は別々に描いてから合成出来ることを知っておくと、 自由度が上がるかも。)
- (b)
- 円錐を描け。
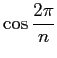 (
(
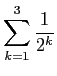 ,
,
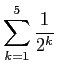 ,
,
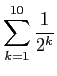 ,
,
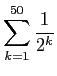 を計算せよ (なるべくユーザー定義関数を使うこと)。
また、それらの値を正確に小数に直せ
(十進法では有限小数というのはすぐ分かりますね?)。
を計算せよ (なるべくユーザー定義関数を使うこと)。
また、それらの値を正確に小数に直せ
(十進法では有限小数というのはすぐ分かりますね?)。
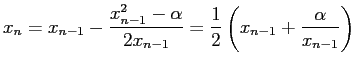 |
図1の描き方のヒント:
球面を描く例は解説文書の中にある (そこではパラメーター曲面としてだったけれど、
レベル・セット (等値面) としても描画可能)。
それを少し修正すれば
![]() を描くのは簡単である。
一方で平面を描くのも簡単 (グラフとして描いたり、
やはりレベル・セット (等値面) としても描画可能)。
同時に描ければ良いけれど、
それは簡単ではないかもしれない。
そういう困難を解決する手段が、
別々に描いておいたものをまとめて表示する Show[] です。
を描くのは簡単である。
一方で平面を描くのも簡単 (グラフとして描いたり、
やはりレベル・セット (等値面) としても描画可能)。
同時に描ければ良いけれど、
それは簡単ではないかもしれない。
そういう困難を解決する手段が、
別々に描いておいたものをまとめて表示する Show[] です。
補足 (2012/6/27)
g1=Plot3D[...] ... g=Show[g1,g2] |
Export["kadai9graph.eps", g] |
Export["syori2/kadai9graph.eps", g] |
Export["syori2/kadai9graph.jpg", g] |
| コマンドプロンプトにて JPEG から PostScript に変換 |
jpeg2ps kadai9graph.jpg > kadai9graph.eps(jpeg2ps コマンドは Windows 標準のコマンドではないが、 2012年度情報処理教室の環境には用意されている。) |
\usepackage[dviout]{graphicx}% もしかすると dviout は dvipdfm が良いかも。
...
\begin{document}
...
\includegraphics[width=10cm]{kadai9graph.eps}
|