-- ある意味では、個々の問題の確率の定義は確率論の外にある --
確率とは、事象の確からしさを表わす尺度で、0 以上 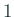 以下の値を取
り、必ず起こる事象の確率は
以下の値を取
り、必ず起こる事象の確率は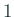 , 起こらない事象の確率は 0, などの性質
を持っている。
, 起こらない事象の確率は 0, などの性質
を持っている。
| Laplace による素朴な確率の定義 |
Laplace は、標本空間が
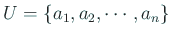 で、根元事象 で、根元事象
が同様に確からしい6とき、
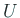 の事象 の事象 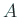 の確率 の確率 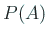 を、 を、
と定義した。
|
![\begin{jexample}[正しいサイコロ]\upshape
\index{ただしいさいころ@...
...\{6\})
\end{displaymath}であるということである。 \qed
\end{jexample}](img44.gif)
- 現実世界の「試行」について、標本空間の設定は色々考えられるが、上のよ
うにして確率を定めるためには、根元事象がいずれも同様に確からしいように
する必要がある。例えば、二枚のコインを投げて、表裏を調べる場合に、標本
空間として
というのを考えると、根元事象は同様に確からしくはならない。二つのコイン
に区別をつけて -- 例えばコイン A とコイン B --、試行の結果を
というように結果を表わす、すなわち
を標本空間とすると、根元事象は同様に確からしくなる。
- 上にあげた「素朴な確率の定義」では、例えば
となっているような「正しくない」いびつなサイコロを扱うことが難しくなっ
てしまう。そこで、現代の確率論では、個々の問題における確率法則 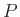 の
決め方については言及せず、ただ
の
決め方については言及せず、ただ 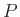 の満たすべき法則だけを指定し、そこ
から導かれることを論じる。
の満たすべき法則だけを指定し、そこ
から導かれることを論じる。
桂田 祐史
![]() 以下の値を取
り、必ず起こる事象の確率は
以下の値を取
り、必ず起こる事象の確率は![]() , 起こらない事象の確率は 0, などの性質
を持っている。
, 起こらない事象の確率は 0, などの性質
を持っている。
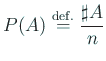
![\begin{jexample}[正しいサイコロ]\upshape
\index{ただしいさいころ@...
...\{6\})
\end{displaymath}であるということである。 \qed
\end{jexample}](img44.gif)