D. 余談: 疾病に対する検査の感度・特異度・陽性的中率

この文書は、もともとは20年以上前に書いた授業で使うためのノートであり、 長い間放置していた。私の専門は確率・統計とは縁遠いので、 確率のことを考えるのは入試関係の仕事をしているときくらい。 ところで現在 (2021/8/26) は、COVID19 流行の真っ只中、 久しぶりに確率の計算をしたので、メモを「余談」として残しておく。

元ネタは次の二つ。

(a)

「統計ナビ 「10-6. ベイズの定理の使い方」」
https://bellcurve.jp/statistics/course/6448.html

(b)

「東京大学保健センター＜コラム＞感度・特異度と陽性的中率」
https://www.hc.u-tokyo.ac.jp/covid-19/tests/

まず (a) の内容を、この文書の記号を使って説明しよう。

日本人の$0.01\%$が罹患している病気があり、 ある検査方法で検査すると、 実際に病気に罹患している人が陽性と判定される確率が$95\%$ ($5\%$ の人は罹患しているにもかかわらず(誤って？)陰性と判定される), 罹患していない人が陰性と判定される確率が$80\%$ ($20\%$ の人は罹患していないにもかかわらず(誤って)陽性と判定される) とされている。ある人がこの病気の検査を受けて陽性という判定を受けたとき、 本当にこの病気に罹患している確率はいくらか。

(脱線) 私事になるが、ずっと昔、 私の家族がある癌の検査を受けて陽性と判定された時、 検査結果の紙に似たような数値とその説明が書いてあった (確率の値は覚えていない)。 ちなみに実際には癌でなかったようだ (その後に受けた別の検査では癌でないという判定結果が出て、 それから現在にいたるまで 20年以上何も対処せず、健康上の問題は特にない。 癌ではなかったと考えている。)

検査で陽性になる事象を $A$, 実際に病気に罹患している事象を$B$とする。 求めよと要求されているのは、いわゆる “陽性的中率” (定義は後述)、 式で書くと $P_A(B)$ であり、与えられている情報は

$$P(B)=0.01\%=0.0001,\quad P_B(A)=95\%=0.95,\quad P_{\overline{B}}(\overline{A})=80\%=0.80.$$

後者から

$$P_{\overline{B}}(A)=1-P_{\overline{B}}(\overline{A})=1-0.80=0.20,\quad P(\overline{B})=1-P(B)=1-0.0001=0.9999.$$

ゆえに

$$P(A) =P(A\cap(B\cup \overline{B})) =P(A\cap B)+P(A\cap \overline{B})$$

$$=P_B(A)P(B)+P_{\overline{B}}(A)P(\overline{B})$$

$$=0.95\cdot 0.0001+0.20\cdot0.9999 =0.200075.$$

Bayesの定理によって

$$P_A(B)=\frac{P(A\cap B)}{P(A)}=\frac{P_B(A)P(B)}{P(A)} =\frac{0.95\cdot 0.0001}{0.20075}=0.000474822\kinji 0.047\%.$$

(病気である確率が、検査をする前($0.0001$) と比べて、 5倍弱大きくなった ($0.00047$) けれど、 もともと確率が低いので、それほど心配する必要はない。)

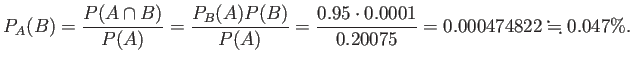
(a) によると

「したがってこの検査法の場合、 陽性という判定を受けてもあまり気を病む必要はないかもしれません。」

だそうだ。

(また脱線モード) 癌の判定結果の話に戻ると、 当時はいきなり判定結果を突きつけられてとてもあわてた。 少し考えてから、あれ、実はそれほど心配する必要はないのではと気づいて、 こういう検査にどれくらいの意味があるのかしら (欠陥のある検査法じゃないのか？)。 とにかくもう一度検査をしろということなのかな、 それにしても不親切な説明だな、と思った (私の家族はおびえて帰って来た)。

定性的にまとめると、もともと罹患している確率が非常に低くて、 罹患していない場合に正しく陰性と判定される確率がそれほど高くない場合 (まちがって陽性と判定される可能性が数% とか、数十% とかそれなりにある場合)、 陽性的中率 (陽性と判定された人が本当に病気である確率) は低い、 それほどあわてなくてもよい、ということである。

用語の解説をしておく。

• 「感度（sensitivity, 真陽性率）」： その病気に罹患している人の中で、 検査で陽性になった人の割合
  blue式で書くと $P_B(A)$
• 「特異度（secificity, 真陰性率）」： その病気に罹患していない人の中で、 検査で陰性になった人の割合
  blue式で書くと $P_{ \overline{B}}(\overline{A})$
• 「偽陽性率」：その病気に罹患していない人の中で、検査で陽性になった人の割合
  blue式で書くと $P_{\overline{B}}(A)=1-P_{\overline{B}} (\overline{A})=1-$特異度
• 「偽陰性率」： その病気に罹患している人の中で、 検査で陰性になった人の割合
  blue式で書くと $P_B(\overline{A})=1-P_B(A)=1-$感度
• 「陽性的中率」: 検査で陽性になった人の中で、 実際にその病気に罹患している人の割合
  blue式で書くと $P_A(B)$

感度も特異度も高い(1に近い)方が検査として優れているということになる。

率直に言って、普段使っていない用語なので、 式を使って考える方が簡単に感じる。

感度 $P_B(A)$ を $k$, 特異度 $P_{\overline{B}}(A)$を $t$, 陽性的中率 $P_A(B)$を $p$ と書くことにする。 検査を受けた人全体の中に占める割合 $P(B)$ (後で説明する東大保健センターの文書の罹患率に相当？) を $r$ とすると、 上に書いた議論は次のようにまとめられる。

$$p=P_A(B)=\frac{P_B(A)P(B)}{P_B(A)P(B) +P_{\overline{B}}(A)P(\overline{B})} =\frac{k r}{kr+(1-t)(1-r)}.$$ (8)

(本当は、英単語の綴りで文字を選択しようと考えたが、 感度も特異度も s で始まるのであきらめた。)

一般に $0\le p\le 1$ である。$p$ は$1$に近いのが検査としてのぞましい。 $t=1$ ならば $p=1$ である(まあ当たり前)。 罹患率 $r$ が小さい、つまり $1-r\kinji 1$ が良い近似である場合は $(1-t)(1-r)\kinji 1-t$. さらに $kr\ll 1-t$ とみなせるので

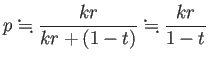$$p\kinji \frac{kr}{kr+(1-t)}\kinji\frac{kr}{1-t}$$   (等式でないので無条件で信用しないこと)$$.$$

上の (a) の例では、$r=0.0001$, $k=0.95$, $t=0.8$ であるから

$$\frac{kr}{1-t}=\frac{0.95\cdot 0.0001}{1-0.8}=0.000475.$$

これは近似なしで得た値 $0.0004748\cdots$ とよく合っている。 この (a) の内容には納得できた (明快な解説である)。

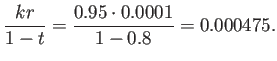
(b) の内容の紹介。一見 (a) と似たような内容だけれど、 微妙に異なるところもあって、 それは最初気づかなかったので、一応フォローしてみる。

「新型コロナウイルス感染症も含め、 疾患の検査にはその精度を検証する必要があります。 その指標として感度、特異度、陽性的中率などがあります。」
(中略) 「陽性的中率は検査で陽性の人の中で実際にその病気に罹患している人の割合です。」 「以下の仮想例（罹患率10%、感度70%、特異度99%）を想定して、 具体的な計算法を記載します。検査を受けた1000人あたりの罹患者を 100人 (罹患率10%) とした場合」

ここでは(8)で陽性的中率を求めることにする。 $r=0.10$, $k=0.70$, $t=0.99$ であるから、陽性的中率は

$$p=\frac{kr}{kr+(1-r)(1-t)}=0.886076\kinji 0.89.$$

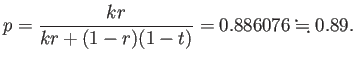
つまり、検査を受けた人のうち、真の罹患者は、89%ということになります。

なるほど。

この陽性的中率は、罹患率によって変化します。 red罹患率が低下すると、 陽性的中率も低下することになります。PCR検査をより多くの人に施行すると、 その集団内での罹患率は低下することが予想されるので、陽性的中率は低下、 つまり実際には罹患していないにもかかわらず陽性と判定される人が増加することになります。

「罹患率が低下すると、 陽性的中率も低下することになります。」とあるのは、 少し考えると一理あるように思える。 例えば $k$, $t$ を定数とするとき

$$\lim_{r\to+0}p(r)=\lim_{r\to+0}\frac{kr}{kr+(1-t)(1-r)} =\frac{0}{0+(1-t)(1-0)}=\frac{0}{1-t}=0.$$

あるいは $A:=(1-t)/k$ とおくと

$$p(r)=\frac{1}{1+A(1/r-1)}=\frac{1}{\frac{A}{r}(1-r(1-1/A))} =\frac{r}{A}+O(r^2)$$   ($r\to 0$)$$.$$

しかし、落ち着いて考えてみると、我々は数学の極限の話をしているのだろうか？ それは問題の取り違いではないか、と気づく。

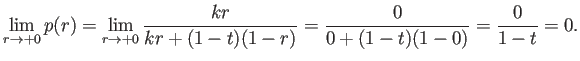
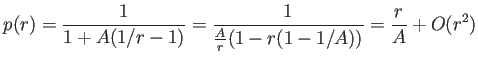後で議論するが、実際には、$r$ は $0.1\%=10^{-3}$ 程度の大きさである一方で、 $t$ は $1-t$ が $10^{-6}$ 程度の大きさとなるくらい $1$ に近かったりする。 その場合は、$A$ は非常に小さく、$p$ は$1$に近い、ということになる。

「PCR検査をより多くの人に施行すると、 その集団内での罹患率は低下することが予想される」を読んで、 $r$ の解釈が (a) とは異なることに気づく。 (a) においては、

$$r=\frac{\text{日本全体での罹患者数}}{\text{日本の総人口}}$$

として議論を始めて、それが検査をした集団内での比率、つまり

$$\frac{\text{検査した集団内での罹患者数}}{\text{検査した人数}}$$

に等しいと暗黙の仮定をおいていたのだろう (定期検診など自覚症状のない人の検査)。

(b) の議論は、 あくまでも検査をした集団内の人達の利益を考えているということになるだろうか。 実際には罹患していないのに、 陽性 (罹患の可能性がある) と判定するのは避けるべきことだ、 という考え方をしている？ そういう考え方は分からないでもない (例えば検査で不安になった我が身を振り返ってそう思う)。

一方で、次の批判は可能であろう。 検査をしていない集団内の罹患者のことは考えていない (発見して治療を受けてもらうべきではないのか。 特に検査を希望していて受けられない人のことはどうか)。 感染症の場合は、それも良くないし、 罹患していない人のことも考えていない (罹患者が発見できなければ感染してしまう危険がある)。

率直に言って、数学以前に問題の設定から考える必要がありそうだ。

以下は、受け売りである。リアルワールドがどうなっているかは ($r$, $k$, $t$ の値は何か)、 数学だけで分かることでないので、「…と言う報告がある。 もしそれが正しければ…ということになる。」を主張するだけである (と言いつつ括弧内で色々つぶやく)。

COVID19のPCR検査の話で言うと、 検体がまともならば、感度も特異度も$1$に非常に近いそうである (原理的に$1$である、という人がいたりする)。

検体の汚染 (というのか感染している他人の検体が混じった)とか、 取り違え(しっかりして欲しい…出来る限り自動化するとか工夫して下さい) とかがなければ、偽陽性は発生せず、 特異度は“実際上は” $1$ とみなして良いと。 実際、特異度は $99.999x\%$ とか非常に高いらしい (最初中国からの報告でそういう値を見た。 その時は本当かなあと思ったが (半信半疑)、 それを裏付ける話はその後も色々あって、 最近の日本でも、 オリンピック選手達を高頻度で検査した結果から同じような値が出ている)。 その結果導かれるのは、陽性的中率は非常に高いということである (実際上偽陽性は心配ない)。

一方、感度の方はそれほど高くないそうだ。実際には感染していても、 ウイルスが局在しているせいで、 ウイルスを含む細胞が採取されるとは限らない。 そのために偽陰性が発生する。実際上の感度は $0.95$ とかそういうものらしい。 この問題は、怪しければ複数回検査するとか、 医師が他の要素も見て判断するとかして克服すべきものなのだろうか。 検疫を設計するのはなかなか難しそうだ。