Next: 3 細かい工夫 周期関数の定義 Up: 1 Mathematica で Fourier級数 Previous: 1 Mathematica で用意されている Fourier 級数関係の関数
周期 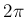 の関数
の関数 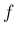 ,
, 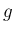 を
を
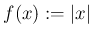 ( (
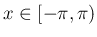 ) )![\begin{align*},\quad
g(x):=
\left\{
\begin{array}[tb]{ll}
-1 & \text{($x\in(-\pi...
...text{($x=0,-\pi$)} \\
1 & \text{($x\in(0,\pi)$)}
\end{array}\right.\end{align*}](img24.png) |
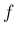 と
と 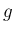 の Fourier 級数の部分和のグラフを描いてみよう。
の Fourier 級数の部分和のグラフを描いてみよう。
講義ノート桂田 [1] にも書いてあるので、 そちらも参考にして下さい。 直リンを張っておくと、 https://m-katsurada.sakura.ne.jp/fourier/fourier-lecture-notes.pdf#page=16 (ずれるかもしれないけれど)
複数の関数を扱うので、
関数 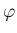 の Fourier 級数を
の Fourier 級数を
$](img26.png) と書くことにしよう。
つまり、
と書くことにしよう。
つまり、
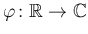 を周期
を周期 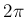 の関数とするとき、
の関数とするとき、
:=\frac{a_0[\varphi]}{2}+\sum_{n=1}^\infty
\left(a_n[\varphi]\cos nx+b_n[\varphi]\sin nx\right),
$](img28.png)
![$\displaystyle \quad
a_n[\varphi]:=\frac{1}{\pi}\int_{-\pi}^\pi \varphi(x)\cos nx\;\Dx,\quad
b_n[\varphi]:=\frac{1}{\pi}\int_{-\pi}^\pi \varphi(x)\sin nx\;\Dx.
$](img29.png)
(関数を明記しようという方針なので、普通は単に 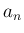 ,
, 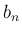 と書くものを、
それぞれ
と書くものを、
それぞれ
![$a_n[\varphi]$](img30.png) ,
,
![$b_n[\varphi]$](img31.png) と書いた。)
と書いた。)
また、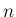 項までの部分和を
項までの部分和を
$](img32.png) と表す。すなわち
と表す。すなわち
:=\frac{a_0[\varphi]}{2}+\sum_{k=1}^n
\left(a_k[\varphi]\cos kx+b_k[\varphi]\sin kx\right).
$](img33.png)
![$S[f]$](img34.png) ,
, ![$S[g]$](img35.png) を自分で計算して求められるようにしておくべきだが、
ここは Mathematica の力を借りてみよう。
を自分で計算して求められるようにしておくべきだが、
ここは Mathematica の力を借りてみよう。
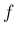 は偶関数であるから
は偶関数であるから ![$b_n[f]=0$](img36.png) である。
である。![$a_n[f]$](img37.png) を求めるには
を求めるには
f0[x_]:=Abs[x] FourierCosCoefficient[f0[x],x,n] FourierCosCoefficient[f0[x],x,0] |
FourierCosCoefficient[f0[x],x,n]
とすると 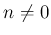 の場合の結果が得られ、
の場合の結果が得られ、
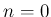 については FourierCosCoefficient[f0[x],x,0] とする必要があるようだ。
については FourierCosCoefficient[f0[x],x,0] とする必要があるようだ。
これで 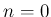 ならば
ならば 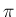 , そうでなければ
, そうでなければ
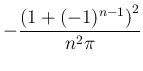 が得られる。すなわち
が得られる。すなわち
![$\displaystyle a_n[f]=
\left\{
\begin{array}[tb]{ll}
\pi& \text{($n=0$)} \\
...
...2k$\ となる $k\in\mathbb{N}$\ が存在するとき)}
\end{array} \right.
\end{array} \right.
$](img41.png)
一方、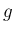 は奇関数であるから
は奇関数であるから ![$a_n[g]=0$](img42.png) である。
である。![$b_n[g]$](img43.png) を求めるには
を求めるには
g0[x_]:=Which[-Pi<x<0,-1,x==0||x==Pi,0,0<x<Pi,1] FourierSinCoefficient[g0[x],x,n] |
![$\displaystyle b_n[g]=\frac{2\left(1+(-1)^{n-1}\right)}{n\pi}
=\left\{
\begin{...
...)}\\
0 & \text{($n=2k$\ となる $k\in\mathbb{N}$\ が存在するとき)}
\end{array} \right.
$](img44.png)
以上から
Mathematica で、
Fourier 級数の 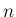 項までの部分和を計算する関数 sf[n,x],
sg[n,x] を作ってみよう。
項までの部分和を計算する関数 sf[n,x],
sg[n,x] を作ってみよう。
![$S[f]$](img34.png) , , ![$S[g]$](img35.png) の部分和を計算する関数を定義 の部分和を計算する関数を定義 |
sf[n_, x_] := Pi/2 - 4/Pi Sum[Cos[k x]/k^2, {k, 1, n, 2}]
sg[n_, x_] := 4/Pi Sum[Sin[k x]/k, {k, 1, n, 2}]
|
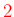 は、
は、
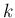 を
を 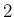 ずつ増やすことを意味する。
ずつ増やすことを意味する。
1変数関数であるから、
グラフを描くには Plot[] を用いれば良い。
周期 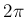 なので、例えば
なので、例えば
![$[-\pi,\pi]$](img50.png) の範囲で描けば十分であるが、
ここでは
の範囲で描けば十分であるが、
ここでは
![$[-3\pi,3\pi]$](img51.png) の範囲で描くことにする
(そうすると、関数が連続であるかどうか、一目見て分かる)。
これは3周期分ということになる。
の範囲で描くことにする
(そうすると、関数が連続であるかどうか、一目見て分かる)。
これは3周期分ということになる。
![$S[f]$](img34.png) , , ![$S[g]$](img35.png) の部分和のグラフを の部分和のグラフを
![$[-3\pi,3\pi]$](img51.png) で描く で描く |
g1=Plot[sf[10,x],{x,-3Pi,3Pi}]
g2=Plot[sg[10,x],{x,-3Pi,3Pi}]
|
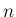 を増やしてどう変わるか見たければ、
Manipulate[] を使うのが便利である。
を増やしてどう変わるか見たければ、
Manipulate[] を使うのが便利である。
![$S[g]$](img35.png) の部分和のグラフ — 項数を増やすとどう変わる? の部分和のグラフ — 項数を増やすとどう変わる? |
Manipulate[Plot[sg[n, x], {x, -Pi, Pi}, PlotPoints -> 200], {n, 1, 100, 1}]
|
桂田 祐史