3 平方根の計算

$c=a+ib$ ( $a,b\in\mathbb{R}$) が与えられた時に、$z^2=c$ の解を $z=x+i y$ ( $x,y\in\mathbb{R}$) の形で求めることが出来る。

(複素数の平方根が、実数の $\sqrt{\mathstrut\quad}$ で表現できる、 という定理に基づく。)

$(x+i y)^2=a+ib$ より連立方程式

$$x^2-y^2=a,\quad 2x y=b$$

が得られるので、その実数の範囲の解を求めれば良い。

$1+i$ の平方根を求めてみよう。

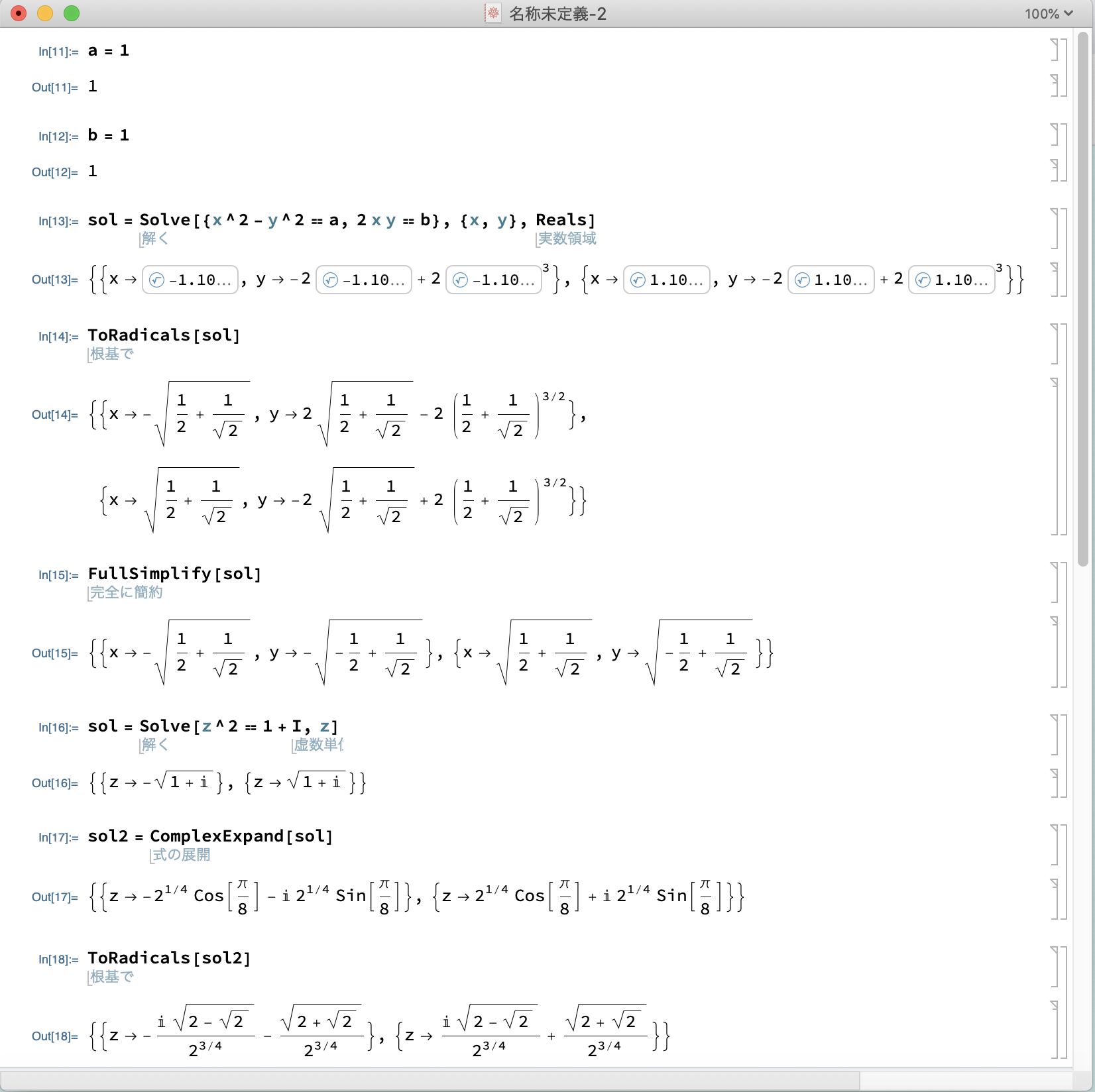
a=1
b=1
sol=Solve[{x^2-y^2==a,2 x y==b},{x,y},Reals]
FullSimplify[sol]

あるいは ToRadicals[sol]

以上は授業で説明したやり方に沿って Mathematica に仕事をさせるものだが、 $z$ の方程式のまま解かせることも出来る (Mathematica が内部で何をしているのかは謎だけど)。

sol=Solve[z^2 == 1 + I, z]
sol2=ComplexExpand[sol]
ToRadicals[sol2]

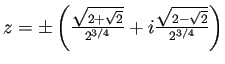最初に $z^2=1+i$ を解かせると $z=\pm\sqrt{1+i}$ となるが、 ComplexExpand[] で実部・虚部に展開させると、 $z=\pm\sqrt[4]{2}\left(\cos\dfrac{\pi}{8}+i\sin\dfrac{\pi}{8}\right)$ となり、ToRadicals[] で処理すると、 $z=\pm\left(\frac{\sqrt{2+\sqrt{2}}}{2^{3/4}}+ i\frac{\sqrt{2-\sqrt{2}}}{2^{3/4}}\right)$ となる。