Next: 6.0.0.1 証明 Up: Laplacian と極座標 Previous: 5 次元における Laplacian の差分近似
![]() の単位球面
の単位球面
![]() の上で定義さ
れたスカラー関数
の上で定義さ
れたスカラー関数 ![]() が与えられているとする。平面領域上の関数と同様に、
が与えられているとする。平面領域上の関数と同様に、
![]() の勾配
の勾配 ![]() なるものが自然に定義できて、
なるものが自然に定義できて、![]() 上のベクトル場
を形成する。
上のベクトル場
を形成する。![]() 上の関数
上の関数 ![]() で
で
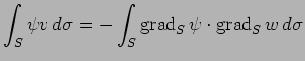
同様にして、任意次元の単位球面における Laplace-Beltrami 作用素が定義 できる。
![\begin{jproposition}[Laplacian と Laplace-Beltrami operator の関係]
$n$\ �...
...面 $S^{n-1}$\ 上の
Laplace-Beltrami 作用素である。
\end{jproposition}](img200.png)
|
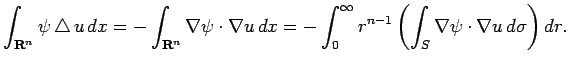
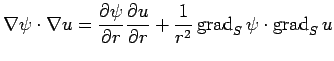
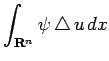 |
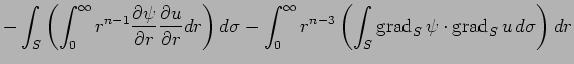 |
||
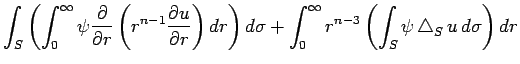 |
|||
![$\displaystyle \int_{\R^n}\psi
\left[
\frac{1}{r^{n-1}}\frac{\rd}{\rd r}
\left(r^{n-1}\frac{\rd u}{\rd r}\right)
+\frac{1}{r^2}\Laplacian_S u
\right]\Dx.$](img207.png) |
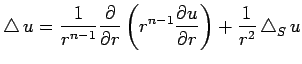
![]() ,
, ![]() の場合に得られている Laplacian の極座標表示から、
Laplace-Beltrami 作用素の公式が得られる。
の場合に得られている Laplacian の極座標表示から、
Laplace-Beltrami 作用素の公式が得られる。
![\begin{jcorollary}[$2$, $3$\ 次元の Laplace-Beltrami 作用素]
$\R^n$\ ($n=...
...phi^2}
& \mbox{($n=3$)}.
\end{array} \right.
\end{displaymath}\end{jcorollary}](img210.png)
|
![\begin{jcorollary}[$r$\ のみによる調和関数]
$\R^n\setminus\{0\}$\ に�...
...x{($n\ne 2$)}
\end{array} \right.
\end{displaymath}となる。
\end{jcorollary}](img211.png)
|