

Next: 3.2 局所離散化誤差、公式の次数
Up: 3.1 多段法, 段数
Previous: 3.1 多段法, 段数
Euler 法、Runge-Kutta 法がこの形になっていることを確かめよ。
- 上の整数
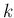 をスキームの段数 (step number) と呼ぶ。
をスキームの段数 (step number) と呼ぶ。
- Euler 法、Runge-Kutta 法では、段数
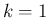 である。
このときは
である。
このときは
という形、つまり
というスキームになる。
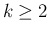 なるスキームを多段法 (multistep method) と呼ぶ。
なるスキームを多段法 (multistep method) と呼ぶ。
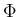 が
が 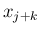 によらないように表される時、
陽解法 (explicit method)であると呼び、
そうでない場合を陰解法 (implicit method) と呼ぶ。
陰解法では
によらないように表される時、
陽解法 (explicit method)であると呼び、
そうでない場合を陰解法 (implicit method) と呼ぶ。
陰解法では 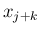 を求めるために、
(一般には非線型の) 方程式を解かねばならないので、
ほとんどの場合に反復法が必要になり、面倒であるが、
次数が高くて安定性のよい方法が作れる。
を求めるために、
(一般には非線型の) 方程式を解かねばならないので、
ほとんどの場合に反復法が必要になり、面倒であるが、
次数が高くて安定性のよい方法が作れる。


Next: 3.2 局所離散化誤差、公式の次数
Up: 3.1 多段法, 段数
Previous: 3.1 多段法, 段数
桂田 祐史
2015-05-30