Next: 8 解析関数の 全体における定積分 Up: 2 次元の数値積分法 Previous: 3 Euler-Maclaurin 展開
この節では「複合」という接頭辞を省いて単に、台形則、中点則、 Simpson 則と呼ぶ。
![]() が周期
が周期 ![]() の周期関数である場合、
の周期関数である場合、![]() 周期にわたる積分
周期にわたる積分
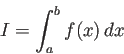
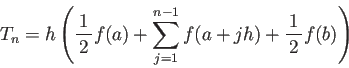
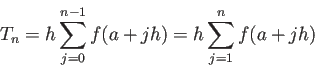
![]() が
が ![]() -級ならば Euler-Maclaurin の公式から、
-級ならば Euler-Maclaurin の公式から、
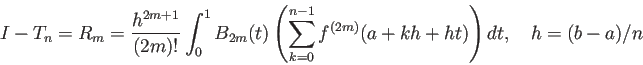
実際に被積分関数の計算回数をそろえて比較すると、 台形則は Simpson 則よりもはるかに高精度の値が得られることが多い。