Next: 3 Euler-Maclaurin ه±•é–‹ Up: 6 Euler-Maclaurin ه±•é–‹ Previous: 1 証وکژ
مپ“مپ®ه°ڈ節مپ®ه†…ه®¹مپ¯و£® [3] مپ«م‚ˆم‚‹م€‚
ه®ںمƒ‘مƒ©مƒ،مƒ¼م‚؟مƒ¼ ![]() م‚’وŒپمپ¤ه½¢ه¼ڈçڑ„ه†ھç´ڑو•°
م‚’وŒپمپ¤ه½¢ه¼ڈçڑ„ه†ھç´ڑو•°
![[*]](footnote.png) :
:
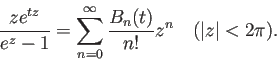
مپ“مپ® ![]() مپ¯
مپ¯ ![]() مپ«مپ¤مپ„مپ¦مپ®
مپ«مپ¤مپ„مپ¦مپ® ![]() و¬،ه¤ڑé …ه¼ڈمپ«مپھم‚‹مپŒم€پ
مپ“م‚Œم‚’
و¬،ه¤ڑé …ه¼ڈمپ«مپھم‚‹مپŒم€پ
مپ“م‚Œم‚’ ![]() و¬،مپ® Bernoulli ه¤ڑé …ه¼ڈمپ¨ه‘¼مپ³م€پ
و¬،مپ® Bernoulli ه¤ڑé …ه¼ڈمپ¨ه‘¼مپ³م€پ
![\begin{jremark}[ç•°مپھم‚‹وµپه„€]\upshape
ن¸ٹمپ«و›¸مپ„مپں Beronoulli و•°مپ®ه®ڑç¾...
...–و–¹مپ«ç§»م‚‹م€‚
\item
ه¥‡و•°ç•ھç›®م‚’飛مپ°مپ™م€‚
\end{enumerate}\end{jremark}](img100.png)

|