Next: 5 力学系とリミット・サイクル Up: 4.3 補足 Previous: 4.3.1 定数係数線形常微分方程式の解の公式, 行列の指数関数
今回の問題を理解するため、行列の指数関数を ![]() の場合に詳しく解析
してみる。
の場合に詳しく解析
してみる。
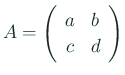 として、
として、
![]() の固有方程式
の固有方程式
![]() の根を判別
して場合分けする。
の根を判別
して場合分けする。
(I) 相異なる 2 実根 ![]() ,
, ![]() を持つ場合
を持つ場合
![]() を
を ![]() に属する
に属する ![]() の固有ベクトルとする(
の固有ベクトルとする(![]() ) とす
ると、
) とす
ると、![]() ,
, ![]() は線形独立になるので、任意の
は線形独立になるので、任意の
![]() は
は
行列の言葉で書くと、
![]() と置くと、
と置くと、
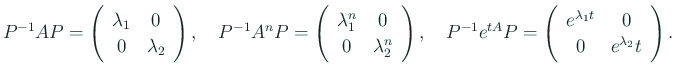
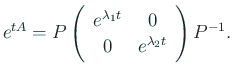
(II) 重根 ![]() を持つ場合
を持つ場合
この場合は、一次独立な固有ベクトルが 2 つ取れるか、1 つしか取れない かで、二つの場合に別れる。
(II-i) 重根 ![]() に属する二つの一次独立な固有ベクトル
に属する二つの一次独立な固有ベクトル ![]() ,
,
![]() が存在する場合
が存在する場合
上と同様にして
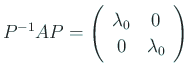 ,
これは実は
,
これは実は
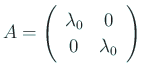 ということだから、
ということだから、
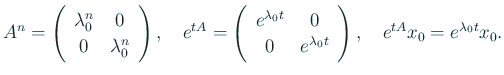
(II-ii) 重根 ![]() に属する一次独立な固有ベクトルが一つしか取
れない場合
に属する一次独立な固有ベクトルが一つしか取
れない場合
仮定より
![]() であり、
であり、
![]() が存在する。そこで
が存在する。そこで
![]() とお
くと
とお
くと ![]() .
.
一方で
![]() である(実際
である(実際 ![]() は固有方程式の
重根だから、固有多項式
は固有方程式の
重根だから、固有多項式
![]() . ゆえに
Hamilton-Cayley の定理から
. ゆえに
Hamilton-Cayley の定理から
![]() .)。よって
.)。よって
![]() すなわち
すなわち
![]() .
.
これと
![]() から
から
![]() とおくと、
とおくと、
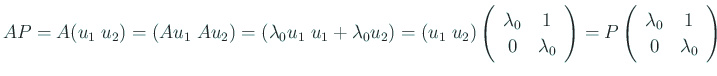 .
. ![]() ,
, ![]() は一次独立
だから
は一次独立
だから ![]() が存在して、
が存在して、
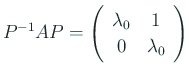 . これから
. これから
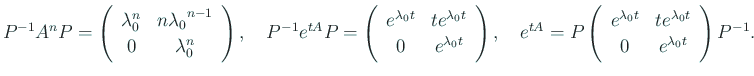
(III) 相異なる 2 虚根
![]() (
(
![]() ,
,
![]() ) を持つ場合
) を持つ場合
![]() に属する固有ベクトルの一つを
に属する固有ベクトルの一つを ![]() (
(
![]() )
とする。
)
とする。
![]() の実部、虚部を取ると、
の実部、虚部を取ると、
![]() ,
,
![]() ,
それで
,
それで ![]() とおくと、
とおくと、
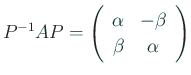 .
これから
.
これから
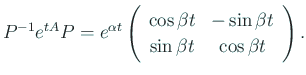
桂田 祐史